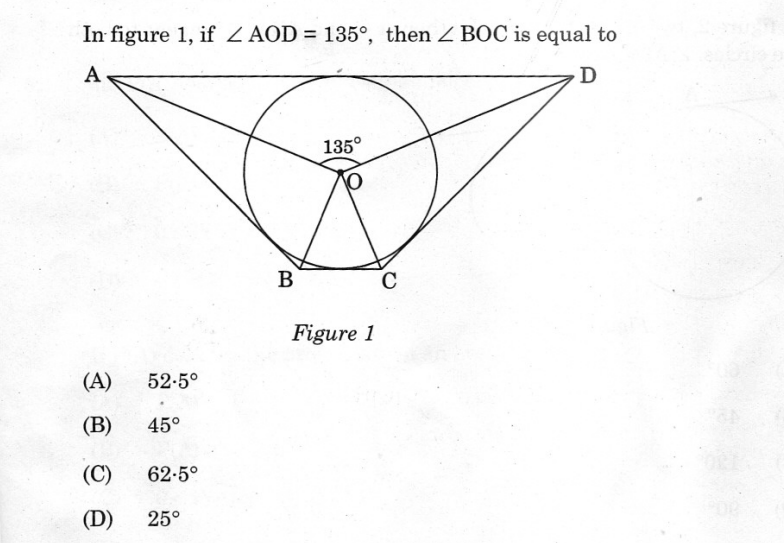
In figure 1, if angle AOD = 135°, then angle BOC is equal to?
Understand the Problem
The question is asking to determine the angle ∠BOC given that angle ∠AOD is 135°. This involves using properties of circles and angles related to intersecting chords.
Answer
The angle ∠BOC is $45^\circ$.
Answer for screen readers
The angle ∠BOC is $45^\circ$.
Steps to Solve
-
Understand the Relationship Between Angles In a circle, if two chords intersect at a point, the angle formed by the chords is related to the angles subtended by the arcs on the circle. Specifically, for angles $\angle AOD$ and $\angle BOC$, they have a relationship where the opposite angles subtend the same arcs.
-
Use the Circle Angle Theorem From the properties of angles in circles, we know that: $$ \angle BOC = \frac{1}{2} \text{(arc BC)} $$ and since $\angle AOD$ also subtends the same arc, we have: $$ \angle AOD + \angle BOC = 180^\circ $$
-
Calculate Angle ∠BOC Given that $\angle AOD = 135^\circ$, we can substitute this into the equation: $$ \angle BOC = 180^\circ - 135^\circ $$ Calculating this gives: $$ \angle BOC = 45^\circ $$
The angle ∠BOC is $45^\circ$.
More Information
The relationship between angles formed by intersecting chords in a circle is an essential concept in circle geometry, and it helps in counting the measures of angles at points of intersection. This specific theorem shows how supplementary angles relate to chord angles.
Tips
One common mistake is to forget that the angles ∠AOD and ∠BOC are supplementary, leading to incorrect calculations. To avoid this, always remember the properties of angles in circles.
AI-generated content may contain errors. Please verify critical information