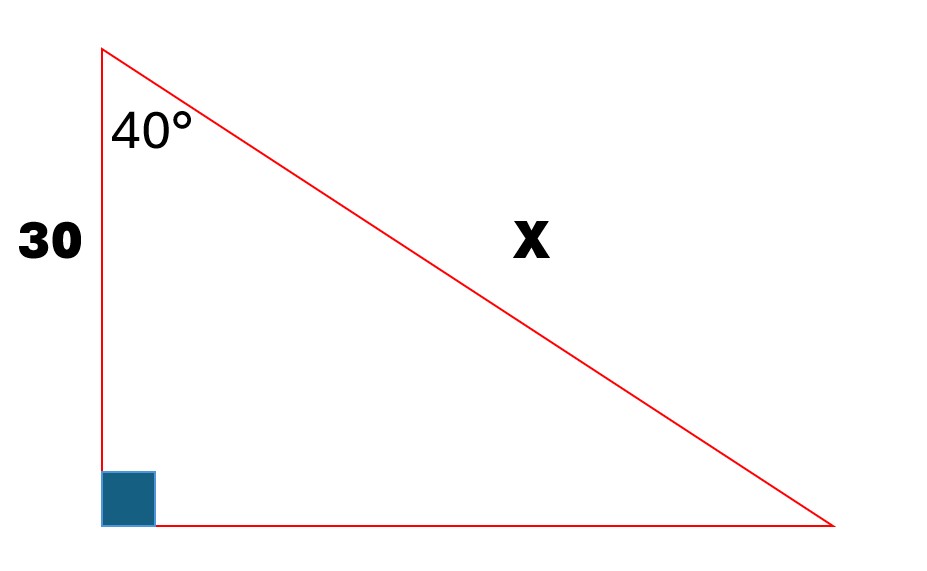
In a right triangle, one angle measures 40 degrees and the opposite side is 30. What is the length of side X?
Understand the Problem
The question involves finding the length of side X in a right triangle where one of the angles is 40 degrees and one of the sides is given as 30 units. This can be solved using trigonometric functions, specifically the sine, cosine, or tangent functions, depending on the relationship between the sides and angles.
Answer
$X \approx 25.173$ units.
Answer for screen readers
The length of side $X$ is approximately $25.173$ units.
Steps to Solve
-
Identify the sides and angle
In this right triangle, we have the angle of $40^\circ$ and the side adjacent to this angle measuring 30 units. -
Determine the trigonometric function to use
Since we need to find the length of side $X$, which is opposite the $40^\circ$ angle, we will use the tangent function. The tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side:
$$ \tan(40^\circ) = \frac{X}{30} $$ -
Rearrange the equation
To find $X$, rearrange the equation:
$$ X = 30 \cdot \tan(40^\circ) $$ -
Calculate the value
Now, calculate $X$ using a calculator to determine $\tan(40^\circ)$:
$$ X \approx 30 \cdot 0.8391 \approx 25.173 $$
The length of side $X$ is approximately $25.173$ units.
More Information
In a right triangle, using trigonometric ratios such as tangent allows us to relate angles to side lengths. The tangent of an angle can be found using calculators or trigonometric tables.
Tips
- Using the wrong trigonometric function: Make sure to identify the correct function based on the sides being used (opposite vs. adjacent).
- Confusing degree measures and radians: Ensure that the calculator is set to the correct mode (degrees) when calculating the tangent.
AI-generated content may contain errors. Please verify critical information