If z = -3 + 4i and zw = -14 + 2i, then w will be:
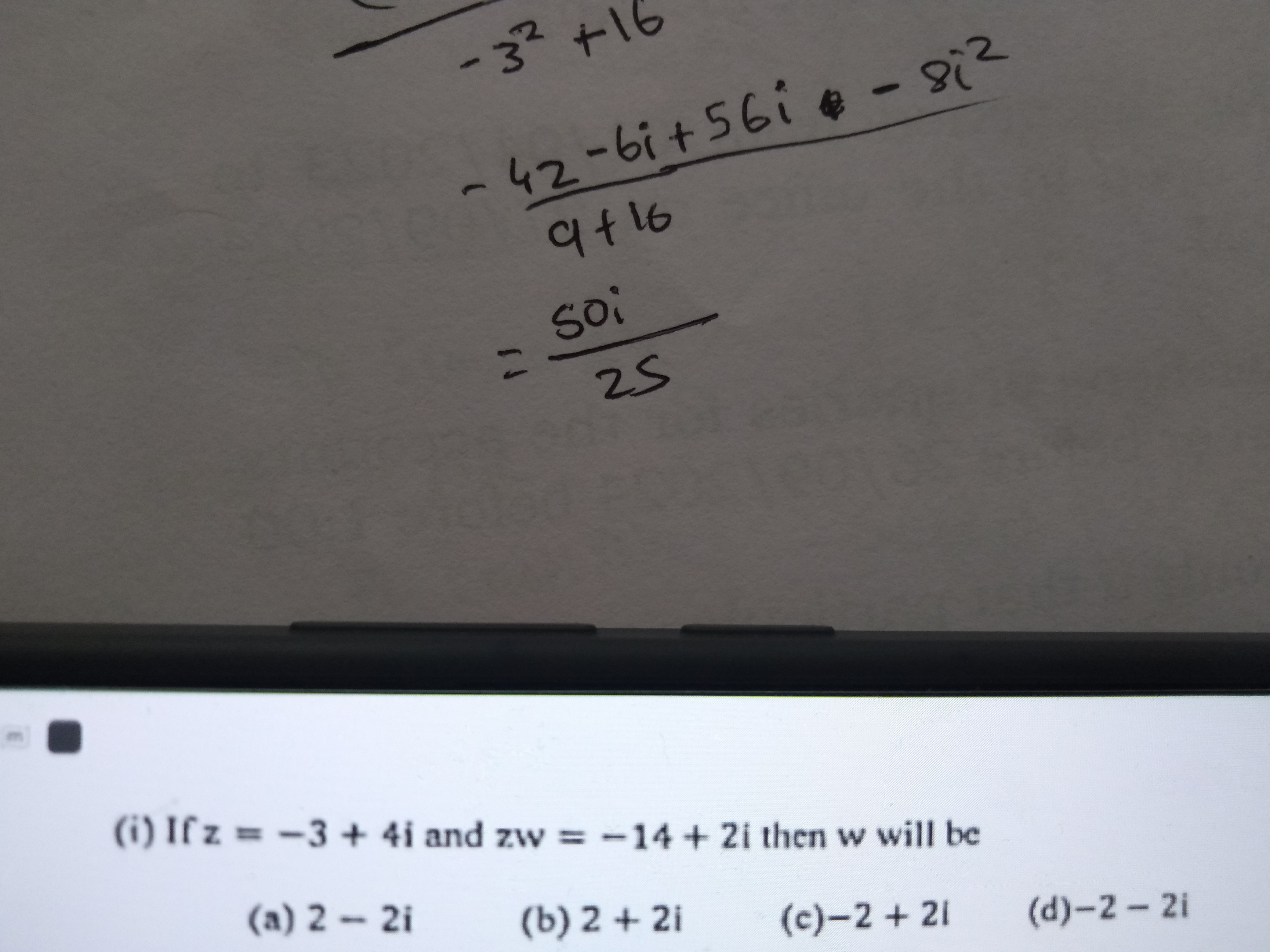
Understand the Problem
The question is asking to find the value of w, given the values of z and zw. It involves complex numbers and requires manipulating these numbers according to the given equation.
Answer
The value of \( w \) is \( 2 + 2i \).
Answer for screen readers
The value of ( w ) is ( 2 + 2i ).
Steps to Solve
- Identify the values of z and zw
Given:
- ( z = -3 + 4i )
- ( zw = -14 + 2i )
- Express w in terms of z and zw
We can find ( w ) by using the formula: $$ w = \frac{zw}{z} $$
- Substitute the known values
Now, substitute the values into the equation: $$ w = \frac{-14 + 2i}{-3 + 4i} $$
- Multiply by the conjugate
To simplify the division, multiply the numerator and the denominator by the conjugate of the denominator: $$ w = \frac{(-14 + 2i)(-3 - 4i)}{(-3 + 4i)(-3 - 4i)} $$
- Calculate the denominator
First, compute the denominator: $$ (-3 + 4i)(-3 - 4i) = (-3)^2 - (4i)^2 = 9 - 16(-1) = 9 + 16 = 25 $$
- Calculate the numerator
Next, compute the numerator: $$ (-14)(-3) + (-14)(-4i) + (2i)(-3) + (2i)(-4i) $$ $$ = 42 + 56i - 6i - 8(-1) $$ $$ = 42 + 50i + 8 = 50 + 50i $$
- Combine to find w
Now substitute back into the equation for ( w ): $$ w = \frac{50 + 50i}{25} $$ $$ = 2 + 2i $$
The value of ( w ) is ( 2 + 2i ).
More Information
This solution highlights the use of complex number division by multiplying by the conjugate. Understanding complex arithmetic is essential for problems involving complex numbers.
Tips
- Forgetting to use the conjugate when dividing complex numbers.
- Miscalculating the multiplication of complex numbers.
- Not simplifying the final expression properly.