Decide if ∑(n=2 to ∞) 1/ln(n!) converges or diverges.
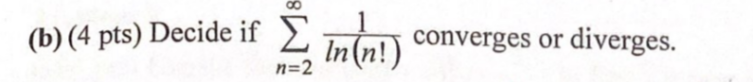
Understand the Problem
The question is asking to determine whether the infinite series starting from n=2 and summing the terms 1/ln(n!) converges or diverges. This involves analyzing the behavior of the series as n approaches infinity.
Answer
The series diverges.
Answer for screen readers
The series (\sum_{n=2}^{\infty} \frac{1}{\ln(n!)}) diverges.
Steps to Solve
- Analyze the term $\ln(n!)$
We will use Stirling's approximation, which states that for large $n$:
$$ \ln(n!) \sim n \ln(n) - n $$
This approximation helps us understand the growth rate of $\ln(n!)$ as $n$ becomes large.
- Rewrite the series term
Using Stirling's approximation, we can rewrite the series term:
$$ \frac{1}{\ln(n!)} \sim \frac{1}{n \ln(n) - n} $$
For large $n$, we can neglect the $-n$ in the denominator, simplifying our term to:
$$ \frac{1}{\ln(n!)} \sim \frac{1}{n \ln(n)} $$
- Determine the behavior of the series
Now, we need to analyze the convergence of the series:
$$ \sum_{n=2}^{\infty} \frac{1}{n \ln(n)} $$
We know that this series diverges by theIntegral Test or the Cauchy Condensation Test.
- Conclusion on convergence
Since
$$ \sum_{n=2}^{\infty} \frac{1}{n \ln(n)} $$
diverges, we conclude that
$$ \sum_{n=2}^{\infty} \frac{1}{\ln(n!)} $$
also diverges.
The series (\sum_{n=2}^{\infty} \frac{1}{\ln(n!)}) diverges.
More Information
The divergence of the series can be tied to the harmonic series behavior. The series involving (\frac{1}{n \ln(n)}) diverges, showing that (\ln(n!)) grows, but not rapidly enough to ensure convergence in the original series.
Tips
- Failing to apply Stirling's approximation correctly or neglecting terms could lead to incorrect conclusions about divergence or convergence.
- Not recognizing that the series (\sum_{n=2}^{\infty} \frac{1}{n \ln(n)}) diverges can mislead one into mistakenly believing that the original series might converge.
AI-generated content may contain errors. Please verify critical information