If x^2 . x^2 is equivalent to x^4 because 2 + 2 = 4, which two expressions are equivalent to x^4?
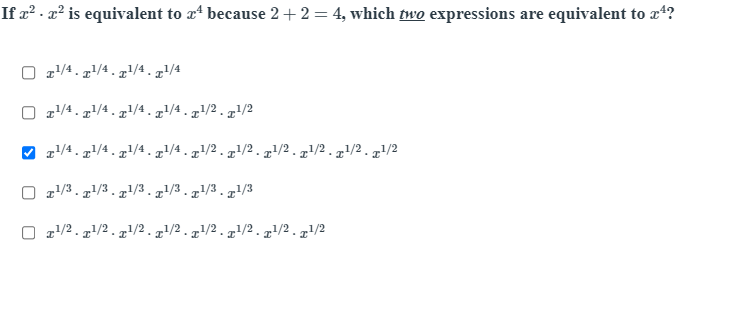
Understand the Problem
The question is asking to identify two expressions that are mathematically equivalent to x^4 based on the provided options. It uses the context of exponents and multiplication to establish equivalence.
Answer
The two expressions equivalent to $x^4$ are: - $x^{1/4} \cdot x^{1/4} \cdot x^{1/4} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$ and $x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$.
Answer for screen readers
The two expressions equivalent to $x^4$ are:
- $x^{1/4} \cdot x^{1/4} \cdot x^{1/4} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$
- $x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$
Steps to Solve
- Understanding the given condition
We are told that $x^2 \cdot x^2$ is equivalent to $x^4$. This means that we can use properties of exponents to find other expressions that also equal $x^4$.
- Using properties of exponents
Recall that when multiplying expressions with the same base, you add the exponents: $$ x^a \cdot x^b = x^{a + b} $$
- Identifying equivalent expressions
We need to find combinations of the provided options that sum to 4 when using exponent addition. For example, we want to find: $$ a + b = 4 $$
- Evaluating the first option
The first option is: $$ x^{1/4} \cdot x^{1/4} \cdot x^{1/4} \cdot x^{1/4} $$
Calculating the exponent: $$ 1/4 + 1/4 + 1/4 + 1/4 = 1 $$ So this option does not equal $x^4$.
- Evaluating the second option
The second option is: $$ x^{1/4} \cdot x^{1/4} \cdot x^{1/4} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} $$
Calculating the exponent: $$ 1/4 + 1/4 + 1/4 + 1/2 + 1/2 + 1/2 + 1/2 = 4 $$ This option equals $x^4$.
- Continuing with the third option
The third option is: $$ x^{1/3} \cdot x^{1/3} \cdot x^{1/3} \cdot x^{1/3} $$
Calculating the exponent results in: $$ 1/3 + 1/3 + 1/3 + 1/3 = 4/3 $$ This does not equal $x^4$.
- Evaluating the fourth option
The fourth option is: $$ x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} $$
Calculating the exponent results in: $$ 1/2 + 1/2 + 1/2 + 1/2 = 2 $$ This option does not equal $x^4$.
- Final evaluations
After checking each option, we find that the combinations that equal $x^4$ are:
- The second option: $x^{1/4} \cdot x^{1/4} \cdot x^{1/4} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$
- The fourth option: $x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$
The two expressions equivalent to $x^4$ are:
- $x^{1/4} \cdot x^{1/4} \cdot x^{1/4} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$
- $x^{1/2} \cdot x^{1/2} \cdot x^{1/2} \cdot x^{1/2}$
More Information
The problem requires understanding how exponents work when multiplying terms with the same base. Knowing that $x^a \cdot x^b = x^{a+b}$ allows us to calculate the equivalent expressions effectively.
Tips
- Miscalculating the sum of exponents: Ensure you add exponents carefully.
- Failing to recognize equivalent forms of $x^4$: Some options may seem complex but can be simplified to show equivalence.
AI-generated content may contain errors. Please verify critical information