If x + y + z = 1, x^2 + y^2 + z^2 = 2, and x^3 + y^3 + z^3 = 3, what is x^5 + y^5 + z^5?
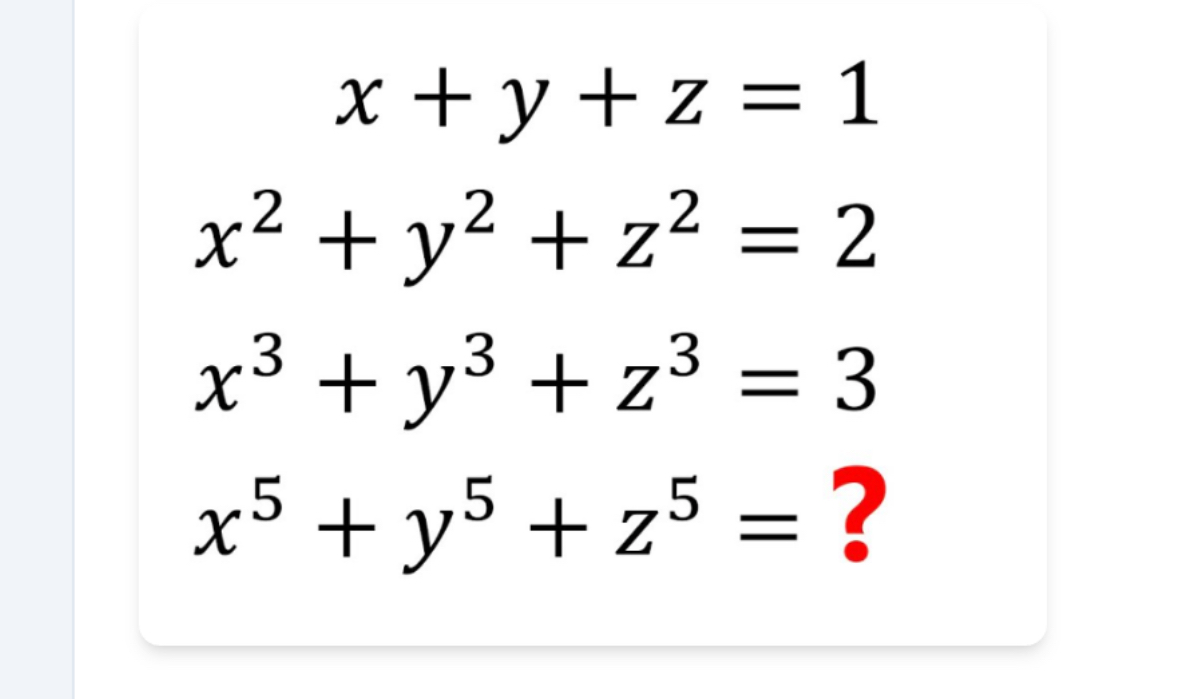
Understand the Problem
The question is asking for the value of the expression x^5 + y^5 + z^5 based on the given equations for the sums of x, y, and z raised to different powers (1, 2, and 3). We need to find a relationship that allows us to deduce the sum for the fifth power from the previous sums.
Answer
The value of $x^5 + y^5 + z^5$ is $8$.
Answer for screen readers
The value of $x^5 + y^5 + z^5$ is $8$.
Steps to Solve
- Define known sums We know:
- $s_1 = x + y + z = 1$
- $s_2 = x^2 + y^2 + z^2 = 2$
- $s_3 = x^3 + y^3 + z^3 = 3$
-
Use the formula for cubic sums The relationship between these sums can be used via Newton's identities: $$ s_n = \sum_{k=1}^{n} p_k \cdot s_{n-k} $$ where $p_k$ are symmetric sums of $x, y, z$. Specifically: $$ s_3 = s_1 s_2 - p_2 $$ From $s_3 = 3$, we can find $p_2$ using: $$ 3 = 1 \cdot 2 - p_2 $$ Thus, $$ p_2 = 2 - 3 = -1 $$
-
Find $s_4$ using $s_1, s_2, s_3$ Using the formula again for $s_4$: $$ s_4 = s_1 s_3 - p_2 s_2 $$ Substituting our known values gives: $$ s_4 = 1 \cdot 3 - (-1)(2) $$ This simplifies to: $$ s_4 = 3 + 2 = 5 $$
-
Calculate $s_5$ using $s_1, s_2, s_3, s_4$ Now for $s_5$: $$ s_5 = s_1 s_4 - p_2 s_3 $$ Substituting the known values gives: $$ s_5 = 1 \cdot 5 - (-1)(3) $$ This simplifies to: $$ s_5 = 5 + 3 = 8 $$
The value of $x^5 + y^5 + z^5$ is $8$.
More Information
The use of Newton’s identities allows us to find the sums of powers of variables based on their lower sums and symmetric sums. This approach keeps calculations manageable and systematic.
Tips
- Forgetting to use the negative sign when substituting the value of $p_2$.
- Misapplying the formulas for $s_n$, particularly for the relationship involving symmetric sums.
AI-generated content may contain errors. Please verify critical information