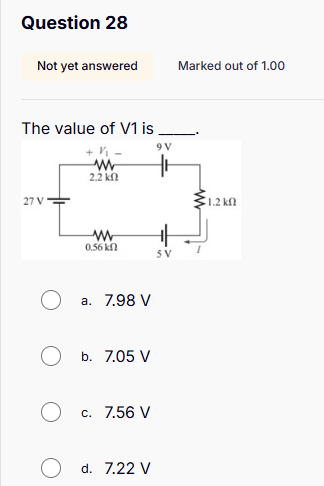
The value of V1 is ____.

Steps to Solve

1. Identify Given Values
   We need to identify the voltages and resistances in the circuit.

• Voltage sources: ( 27 , V ) and ( 5 , V )
• Voltage drop: ( 9 , V )
• Resistor values: ( 2.2 , k\Omega ), ( 0.56 , k\Omega ), and ( 1.2 , k\Omega )

2. Apply Kirchhoff's Voltage Law
   According to Kirchhoff's Voltage Law, the sum of all voltages in a closed loop must equal zero. The loop can be expressed as: $$ 27 , V - V_1 - 9 , V - \left( I \cdot 2.2 \times 10^3 \Omega \right) - 5 , V = 0 $$

3. Calculate Total Resistance and Current
   We need to calculate the total resistance in the circuit using: $$ R_{total} = 2.2 , k\Omega + 0.56 , k\Omega + 1.2 , k\Omega = 4.96 , k\Omega $$
   Then, calculate the current ( I ) using Ohm's Law: $$ I = \frac{V_{total}}{R_{total}} = \frac{27 , V - 5 , V}{4.96 , k\Omega} $$

4. Calculate Voltage Drop across ( 2.2 , k\Omega )
   The voltage drop across the ( 2.2 , k\Omega ) resistor can be calculated as: $$ V_{drop} = I \cdot R = I \cdot 2.2 , k\Omega $$

5. Find ( V_1 )
   Substituting the current value back into the equation we formed in step 2 allows us to find ( V_1 ): $$ V_1 = 27 , V - 9 , V - V_{drop} - 5 , V $$