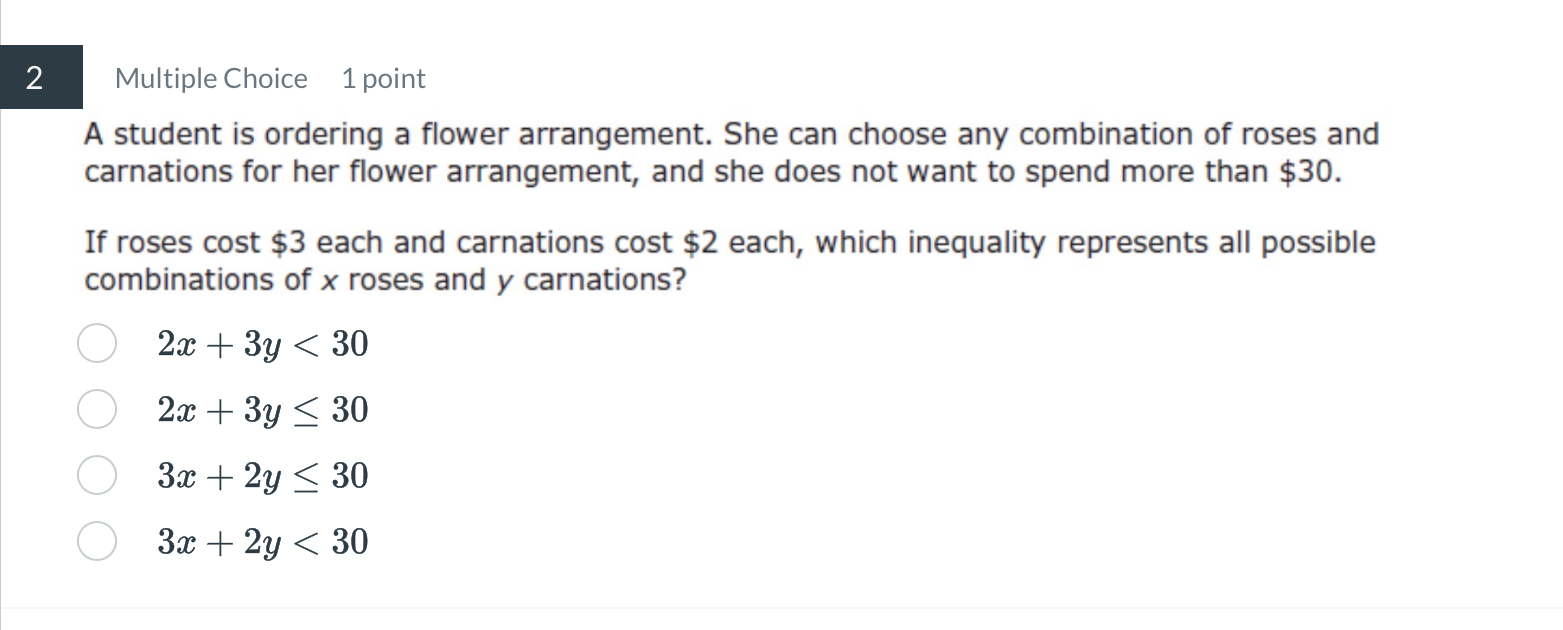
If roses cost $3 each and carnations cost $2 each, which inequality represents all possible combinations of x roses and y carnations?
Understand the Problem
The question is asking to find the inequality that represents all possible combinations of roses and carnations the student can buy without exceeding a budget of $30, given the prices of the flowers.
Answer
$$ 3x + 2y \leq 30 $$
Answer for screen readers
The inequality that represents all possible combinations of ( x ) roses and ( y ) carnations is: $$ 3x + 2y \leq 30 $$
Steps to Solve
- Identify the costs of each flower Roses cost $3 each, and carnations cost $2 each. Therefore,
- If we let ( x ) represent the number of roses, the cost for roses is ( 3x ).
- Let ( y ) represent the number of carnations, the cost for carnations is ( 2y ).
-
Set up the inequality for the total cost The total cost for ( x ) roses and ( y ) carnations should not exceed $30. Thus, we can express this as: $$ 3x + 2y \leq 30 $$
-
Select the correct inequality from the options given To find out which of the listed inequalities is correct, we rewrite our derived inequality ( 3x + 2y \leq 30 ). Among the provided choices:
- ( 2x + 3y < 30 )
- ( 2x + 3y \leq 30 )
- ( 3x + 2y \leq 30 ) (This is correct)
- ( 3x + 2y < 30 )
The inequality that represents all possible combinations of ( x ) roses and ( y ) carnations is: $$ 3x + 2y \leq 30 $$
More Information
This inequality ensures that any combination of roses and carnations chosen will not exceed the student's budget of $30. The student can purchase multiple types of flowers as long as their total cost remains within this budget.
Tips
- A common mistake might be to mix up the coefficients or signs in the inequality. Be sure to assign the correct costs to each variable before forming the inequality.
- Another mistake could be interpreting "not exceeding $30" as strictly less than, rather than less than or equal to.
AI-generated content may contain errors. Please verify critical information