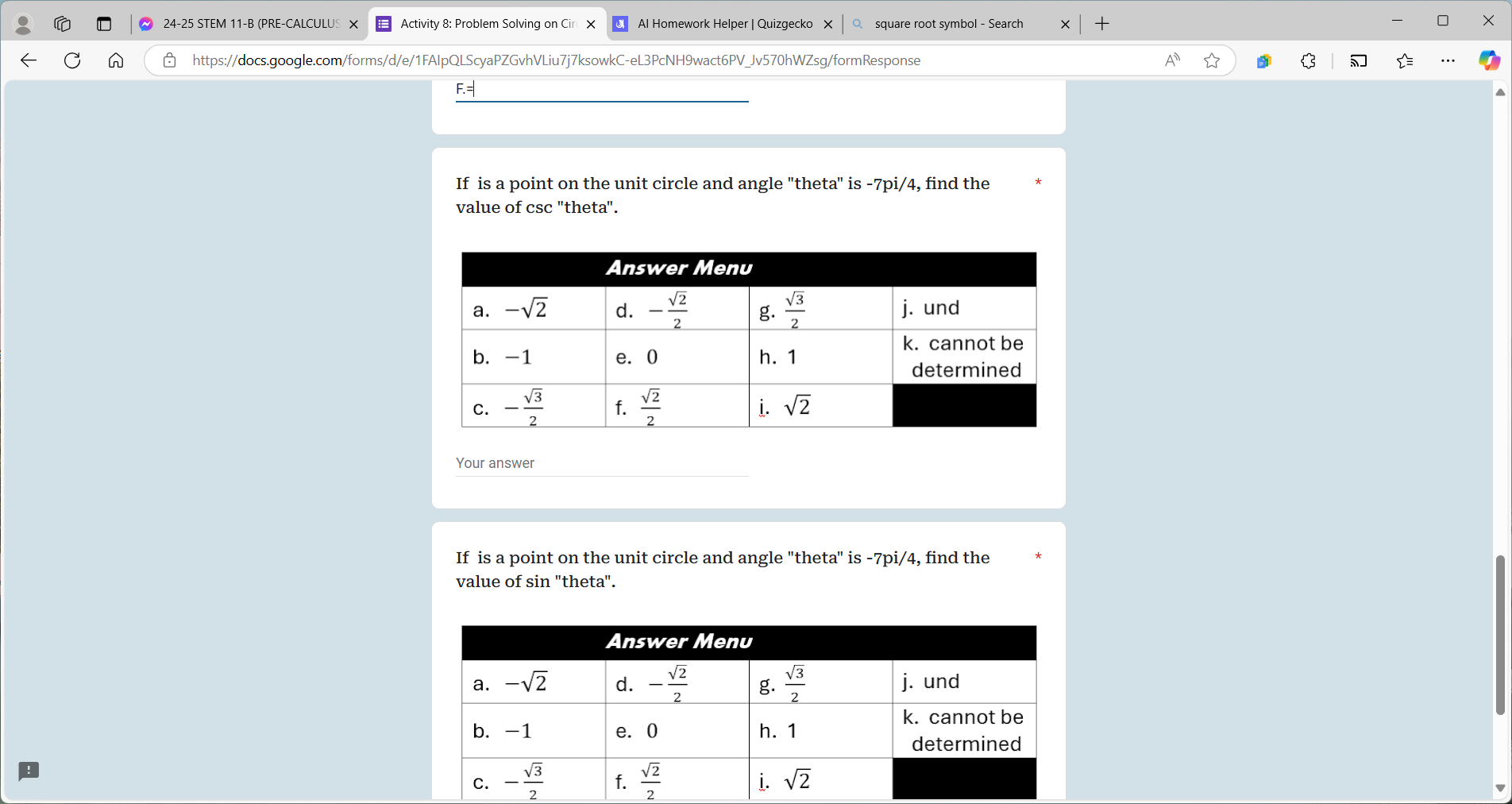
If is a point on the unit circle and angle 'theta' is -7pi/4, find the value of csc 'theta'. If is a point on the unit circle and angle 'theta' is -7pi/4, find the value of sin 'th... If is a point on the unit circle and angle 'theta' is -7pi/4, find the value of csc 'theta'. If is a point on the unit circle and angle 'theta' is -7pi/4, find the value of sin 'theta'.
Understand the Problem
The question is asking for the value of the cosecant and sine functions for a specific angle on the unit circle (-7π/4). We will use the properties of the unit circle and trigonometric identities to find the values.
Answer
$\sqrt{2}$
Answer for screen readers
The value of $\csc\left(-\frac{7\pi}{4}\right)$ is $\sqrt{2}$.
Steps to Solve
-
Identifying the Angle on the Unit Circle To find the values of $\csc\left(-\frac{7\pi}{4}\right)$ and $\sin\left(-\frac{7\pi}{4}\right)$, first convert the angle into a positive angle by adding $2\pi$:
$$ -\frac{7\pi}{4} + 2\pi = -\frac{7\pi}{4} + \frac{8\pi}{4} = \frac{\pi}{4} $$ -
Finding the Sine Value Now, find $\sin\left(\frac{\pi}{4}\right)$ using the unit circle. The coordinates for the angle $\frac{\pi}{4}$ are $(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$. Thus, $$ \sin\left(-\frac{7\pi}{4}\right) = \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} $$
-
Finding the Cosecant Value Next, recall that the cosecant function is the reciprocal of the sine function: $$ \csc\left(\theta\right) = \frac{1}{\sin\left(\theta\right)} $$ So, $$ \csc\left(-\frac{7\pi}{4}\right) = \frac{1}{\frac{\sqrt{2}}{2}} = \frac{2}{\sqrt{2}} = \sqrt{2} $$
The value of $\csc\left(-\frac{7\pi}{4}\right)$ is $\sqrt{2}$.
More Information
The cosecant function is important because it relates to the sine function through reciprocal relationships. The specific angle $-\frac{7\pi}{4}$ corresponds to the same point as $\frac{\pi}{4}$ on the unit circle, leading to the same sine value due to periodicity of trigonometric functions.
Tips
- Confusing sine and cosecant: Remember that $\csc(\theta) = \frac{1}{\sin(\theta)}$.
- Forgetting to convert negative angles to positive ones: Always convert negative angles into the corresponding positive angles on the unit circle.
AI-generated content may contain errors. Please verify critical information