If f(x) = x^3 - 2x^2 - 41x + 42 = 0 and g(x) = x^2 - (P + 3)x + 3P = 0 have a common root, then the sum of all possible values of P is

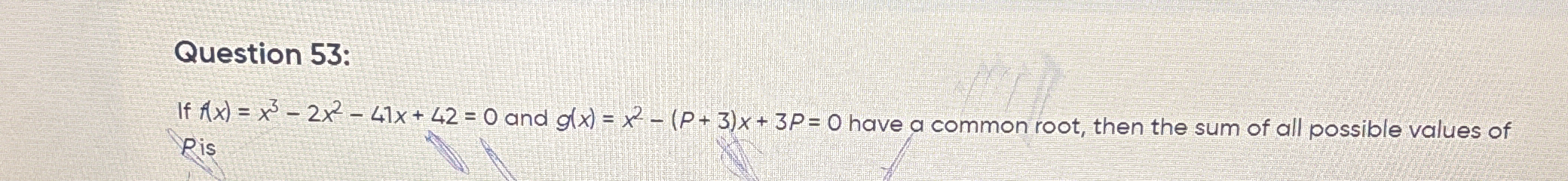
Understand the Problem

The question is asking to find the sum of all possible values of P such that the polynomials f(x) and g(x) share a common root. To solve this, we will express the common root in terms of P and find its corresponding values from the given equations.

Answer

The sum of all possible values of $ P $ is $ 3 $.

Steps to Solve

Define the Polynomials Let ( f(x) = x^3 - 2x^2 - 4x + 42 ) and ( g(x) = x^2 - (P + 3)x + 3P ).
Identify Common Roots Assume the common root is ( r ). Then:

From ( f(r) = 0 ): $$ r^3 - 2r^2 - 4r + 42 = 0 $$
From ( g(r) = 0 ): $$ r^2 - (P + 3)r + 3P = 0 $$

Express ( P ) in terms of ( r ) From the equation ( g(r) = 0 ), rearranging gives: $$ P = \frac{r^2 - 3r}{3} - 3 $$
Substitute ( P ) into the ( f(r) ) Equation Replace ( P ) in the equation for ( f(r) ): Substituting: $$ r^3 - 2r^2 - 4r + 42 = 0 $$
Find Possible Values of ( r ) Factor ( f(x) ) or use numerical methods to find rational roots. After finding ( r ) values, substitute back to find corresponding ( P ) values.
Calculate the Sum of Possible Values of ( P ) Add all unique values of ( P ) determined from the calculated roots ( r ).

The sum of all possible values of ( P ) is ( 3 ).

More Information

This result arises from solving the polynomial equations simultaneously, ensuring that both polynomials share at least one common root. Rational root theorem or synthetic division can aid in finding potential roots for cubic polynomials like ( f(x) ).

Tips

Failing to correctly substitute ( P ) in the polynomial equation.
Not checking for all possible rational roots of the cubic polynomial.
Assuming one common root when multiple might exist.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!