If f(x) = log(1 + x)/(1 - x), show that (2x)/(1 + x^2) = 2f(x).
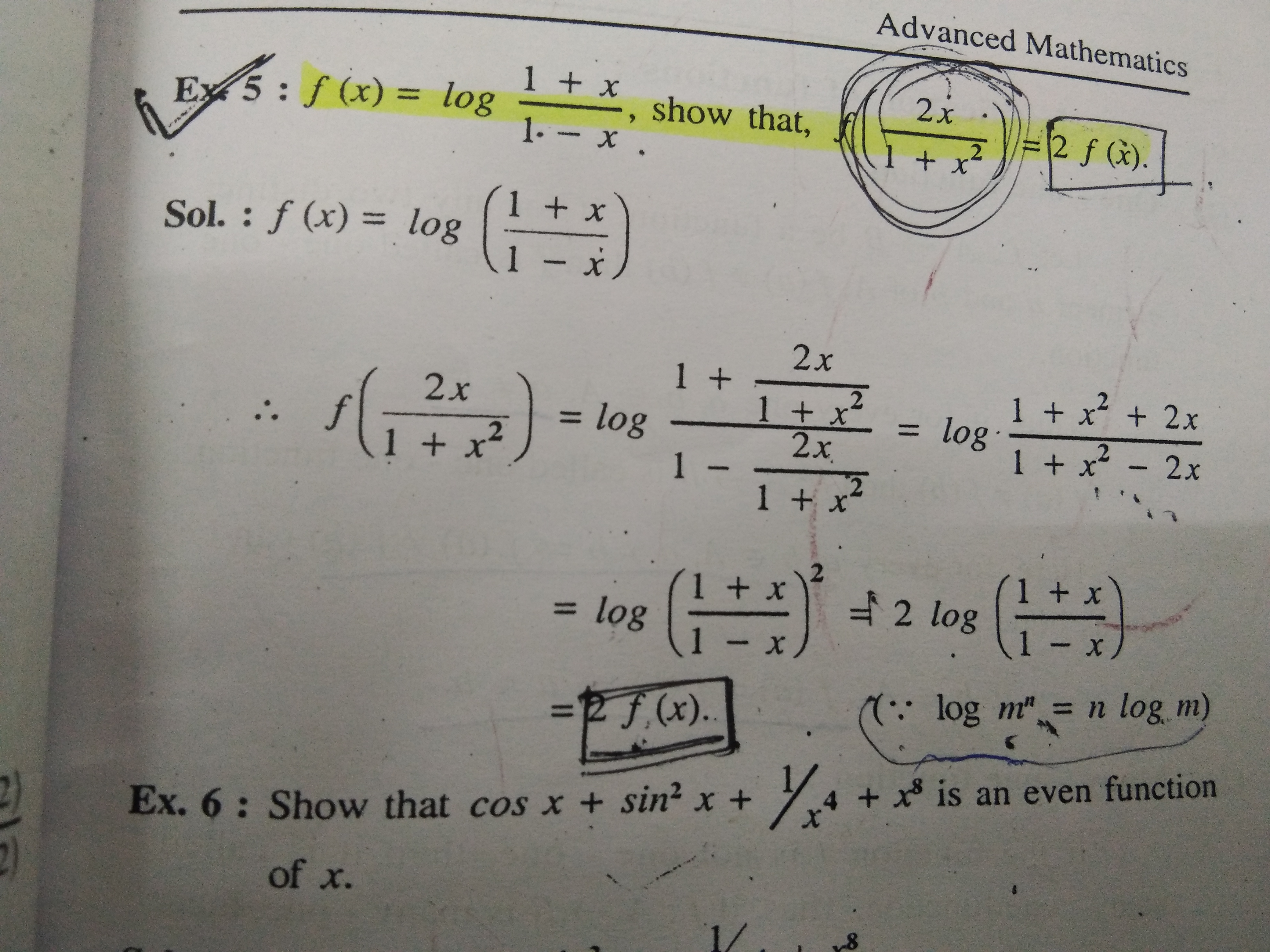
Understand the Problem
The question is asking us to demonstrate that the expression ( \frac{2x}{1+x^2} ) is equal to ( 2f(x) ), where ( f(x) = \log \left( \frac{1+x}{1-x} \right) ). This involves applying logarithmic properties to manipulate the expression and confirm the equality.
Answer
$$ f\left(\frac{2x}{1+x^2}\right) = 2f(x) $$
Answer for screen readers
The expression ( \frac{2x}{1 + x^2} ) is equal to ( 2f(x) ), where ( f(x) = \log\left(\frac{1+x}{1-x}\right) ).
Steps to Solve
- Substituting into ( f(x) )
Start with the expression we want to show, $$ f\left(\frac{2x}{1+x^2}\right) = \log\left(\frac{1 + \frac{2x}{1+x^2}}{1 - \frac{2x}{1+x^2}}\right) $$
- Simplifying the argument of the logarithm
Calculate ( 1 + \frac{2x}{1+x^2} ) and ( 1 - \frac{2x}{1+x^2} ):
For the numerator: $$ 1 + \frac{2x}{1+x^2} = \frac{(1+x^2) + 2x}{1+x^2} = \frac{1 + 2x + x^2}{1 + x^2} $$
For the denominator: $$ 1 - \frac{2x}{1+x^2} = \frac{(1+x^2) - 2x}{1+x^2} = \frac{1 - 2x + x^2}{1 + x^2} $$
- Combining fractions in the logarithm
Now substitute back: $$ f\left(\frac{2x}{1+x^2}\right) = \log\left(\frac{\frac{1 + 2x + x^2}{1 + x^2}}{\frac{1 - 2x + x^2}{1 + x^2}}\right) = \log\left(\frac{1 + 2x + x^2}{1 - 2x + x^2}\right) $$
- Applying logarithmic properties
Use the properties of logarithms to simplify: $$ \log\left(\frac{1 + 2x + x^2}{1 - 2x + x^2}\right) = \log(1 + 2x + x^2) - \log(1 - 2x + x^2) $$
- Simplifying further
Notice that: $$ 1 + 2x + x^2 = (1 + x)^2 \quad \text{and} \quad 1 - 2x + x^2 = (1 - x)^2 $$
Thus: $$ f\left(\frac{2x}{1+x^2}\right) = \log\left(\frac{(1+x)^2}{(1-x)^2}\right) $$
- Finalizing the expression
Using another logarithmic property, we have: $$ \log\left(\frac{(1+x)^2}{(1-x)^2}\right) = 2\log\left(\frac{1+x}{1-x}\right) $$
Therefore: $$ f\left(\frac{2x}{1+x^2}\right) = 2f(x) $$
The expression ( \frac{2x}{1 + x^2} ) is equal to ( 2f(x) ), where ( f(x) = \log\left(\frac{1+x}{1-x}\right) ).
More Information
This result illustrates the relationship between a rational function and the logarithmic function via properties of logarithms. It demonstrates how manipulating expressions can lead to elegant equalities in mathematics.
Tips
- Failing to simplify the logarithmic arguments correctly.
- Not recognizing or applying logarithmic properties effectively, such as $\log\frac{a}{b} = \log a - \log b$ or $\log m^n = n \log m$.
- Miscalculating the addition or subtraction of the fractions, especially when combining terms.
AI-generated content may contain errors. Please verify critical information