If f(x) = 1/(3x + 4) and g(x) = 1/(x - 2), what is f + g?
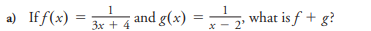
Understand the Problem
The question is asking to find the sum of two functions, f(x) and g(x), provided their definitions. We will need to combine the two functions mathematically to obtain f + g.
Answer
The sum of the functions is $$ f(x) + g(x) = \frac{4x + 2}{(3x + 4)(x - 2)} $$
Answer for screen readers
The sum of the functions is
$$ f(x) + g(x) = \frac{4x + 2}{(3x + 4)(x - 2)} $$
Steps to Solve
- Find a Common Denominator
To add the two functions $f(x)$ and $g(x)$, we need a common denominator. The functions are:
$$ f(x) = \frac{1}{3x + 4} $$
$$ g(x) = \frac{1}{x - 2} $$
The common denominator will be the product of both denominators:
$$ (3x + 4)(x - 2) $$
- Rewrite Each Function
Now we will rewrite each function with the common denominator:
For $f(x)$, multiply the numerator and denominator by $(x - 2)$:
$$ f(x) = \frac{1 \cdot (x - 2)}{(3x + 4)(x - 2)} = \frac{x - 2}{(3x + 4)(x - 2)} $$
For $g(x)$, multiply the numerator and denominator by $(3x + 4)$:
$$ g(x) = \frac{1 \cdot (3x + 4)}{(x - 2)(3x + 4)} = \frac{3x + 4}{(3x + 4)(x - 2)} $$
- Add the Two Functions
Now we can sum the two rewritten functions:
$$ f(x) + g(x) = \frac{x - 2}{(3x + 4)(x - 2)} + \frac{3x + 4}{(3x + 4)(x - 2)} $$
Combine the numerators:
$$ f(x) + g(x) = \frac{(x - 2) + (3x + 4)}{(3x + 4)(x - 2)} $$
- Simplify the Numerator
Combine like terms in the numerator:
$$ (x - 2) + (3x + 4) = 4x + 2 $$
So now we have:
$$ f(x) + g(x) = \frac{4x + 2}{(3x + 4)(x - 2)} $$
The sum of the functions is
$$ f(x) + g(x) = \frac{4x + 2}{(3x + 4)(x - 2)} $$
More Information
This expression represents the combined function of $f(x)$ and $g(x)$. It can be used to evaluate the sum for different values of $x$. This method of combining functions is crucial in algebra, particularly in calculus and for understanding function behavior.
Tips
- Mistaking the common denominator by not multiplying correctly.
- Not simplifying the numerator properly before combining.
- Forgetting to include restrictions on $x$ based on the original functions' domains.
AI-generated content may contain errors. Please verify critical information