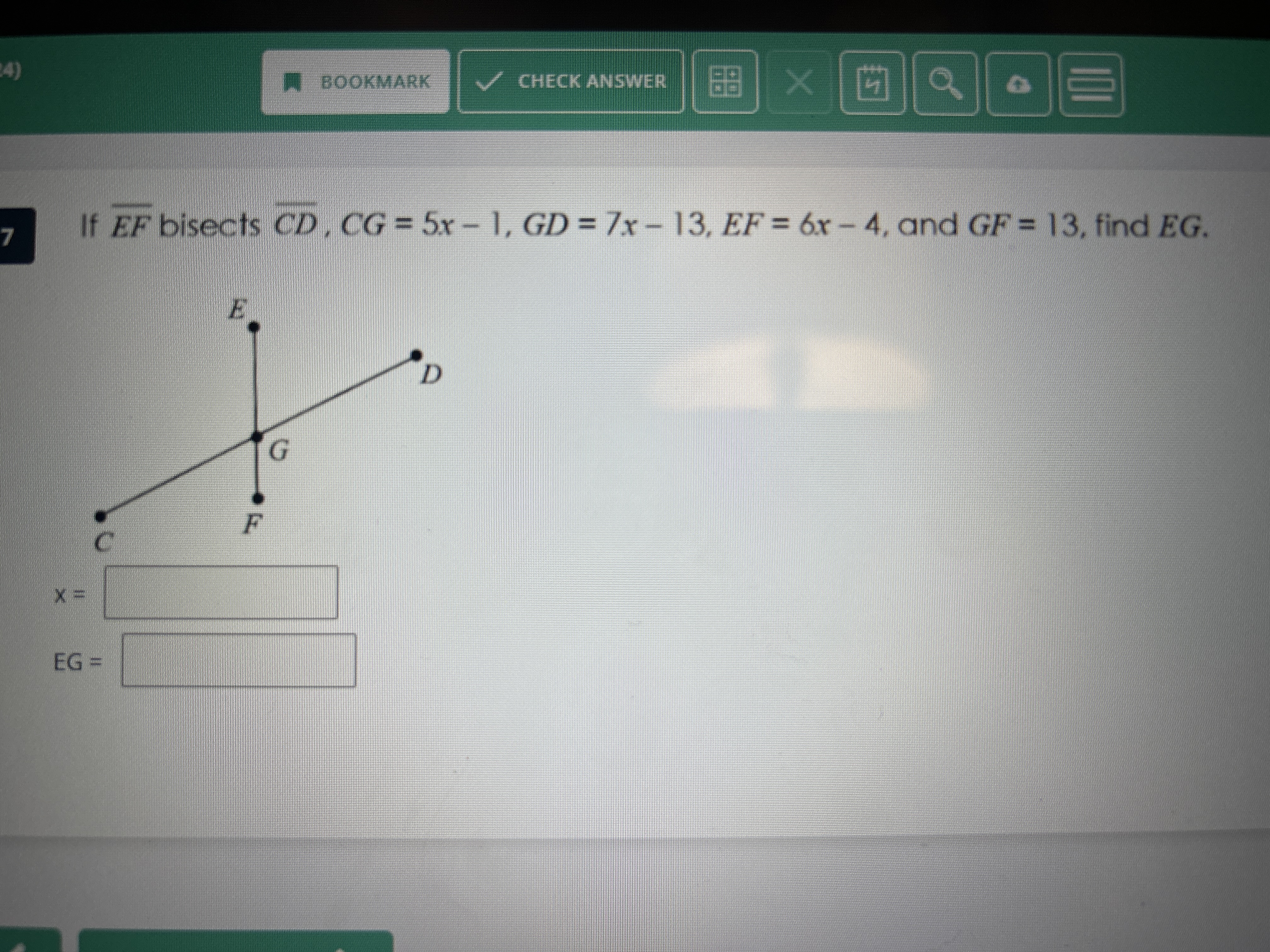
If EF bisects CD, CG = 5x - 1, GD = 7x - 13, EF = 6x - 4, and GF = 13, find EG.

Understand the Problem

The question involves geometry, specifically dealing with a transversal that bisects another line segment. We need to find the value of x and then calculate the length of EG based on given expressions for segments. This requires setting up equations based on the bisection property and solving for the unknowns.

Answer

$ x = \frac{23}{6} $, $ EG = 9.5 $

Steps to Solve

Identify the expressions
We have the following expressions based on the lengths:

( CG = 5x - 1 )
( GD = 7x - 13 )
( EF = 6x - 4 )
( GF = 13 )

Since ( EF ) bisects ( CD ), we can express this relationship as:
$$ CG + GD = CD $$

Set up the equation for ( CD )
Substituting the expressions for ( CG ) and ( GD ):
$$ (5x - 1) + (7x - 13) = CD $$
This simplifies to:
$$ 12x - 14 = CD $$
Substitute ( CD ) with ( EF + GF )
From the problem statement:
$$ CD = EF + GF $$
This can be substituted as:
$$ 12x - 14 = (6x - 4) + 13 $$
Simplify the equation
Now simplifying gives us:
$$ 12x - 14 = 6x + 9 $$
Rearranging yields:
$$ 12x - 6x = 9 + 14 $$
$$ 6x = 23 $$
Solve for ( x )
Finally, we divide by 6:
$$ x = \frac{23}{6} $$
Calculate the length of ( EG )
Using the expression we derived for ( EF ):
$$ EF = 6x - 4 $$
Substituting ( x ):
$$ EF = 6 \left( \frac{23}{6} \right) - 4 $$
This simplifies to:
$$ EF = 23 - 4 = 19 $$
Determine ( EG )
Since ( EG = \frac{EF}{2} ) because ( EF ) bisects:
$$ EG = \frac{19}{2} = 9.5 $$

( x = \frac{23}{6} ) and ( EG = 9.5 )

More Information

The segments defined in the problem represent a typical bisector scenario in geometry, where relationships between segment lengths can be expressed algebraically. Finding the value of ( x ) allows us to compute various segment lengths.

Tips

Mistaking the summative relationship of segments; be careful to correctly apply ( CG + GD = CD ).
Forgetting to appropriately substitute and simplify equations. It's essential to keep track of every step clearly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!