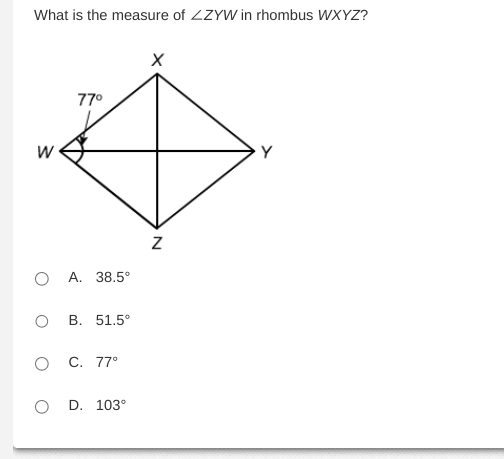
What is the measure of angle ZYW in rhombus WXYZ?
Understand the Problem
The question is asking for the measure of angle ZYW in a rhombus, where the angle WXY measures 77 degrees. Since opposite angles in a rhombus are equal and adjacent angles are supplementary, we can determine the measure of angle ZYW by using the properties of a rhombus.
Answer
The measure of angle $ZYW$ is $103^\circ$.
Answer for screen readers
The measure of angle $ZYW$ is $103^\circ$.
Steps to Solve
- Identify Angle Relationships in a Rhombus
In a rhombus, opposite angles are equal, and adjacent angles are supplementary. Given that $\angle WXY = 77^\circ$, we can determine the adjacent angle $\angle ZYW$.
- Calculate Angle ZYW
Since the angles are supplementary, we can use the equation: $$ \angle WXY + \angle ZYW = 180^\circ $$ Substituting the known value: $$ 77^\circ + \angle ZYW = 180^\circ $$
- Solving for Angle ZYW
To find $\angle ZYW$, we subtract $77^\circ$ from $180^\circ$: $$ \angle ZYW = 180^\circ - 77^\circ $$ Calculating the result: $$ \angle ZYW = 103^\circ $$
The measure of angle $ZYW$ is $103^\circ$.
More Information
In a rhombus, each pair of opposite angles are equal, and each pair of adjacent angles adds up to $180^\circ$. This property helps in determining unknown angles quickly.
Tips
- Forgetting that adjacent angles in a rhombus are supplementary can lead to incorrect angle calculations. Always remember to use the supplementary relationship when working with adjacent angles.
AI-generated content may contain errors. Please verify critical information