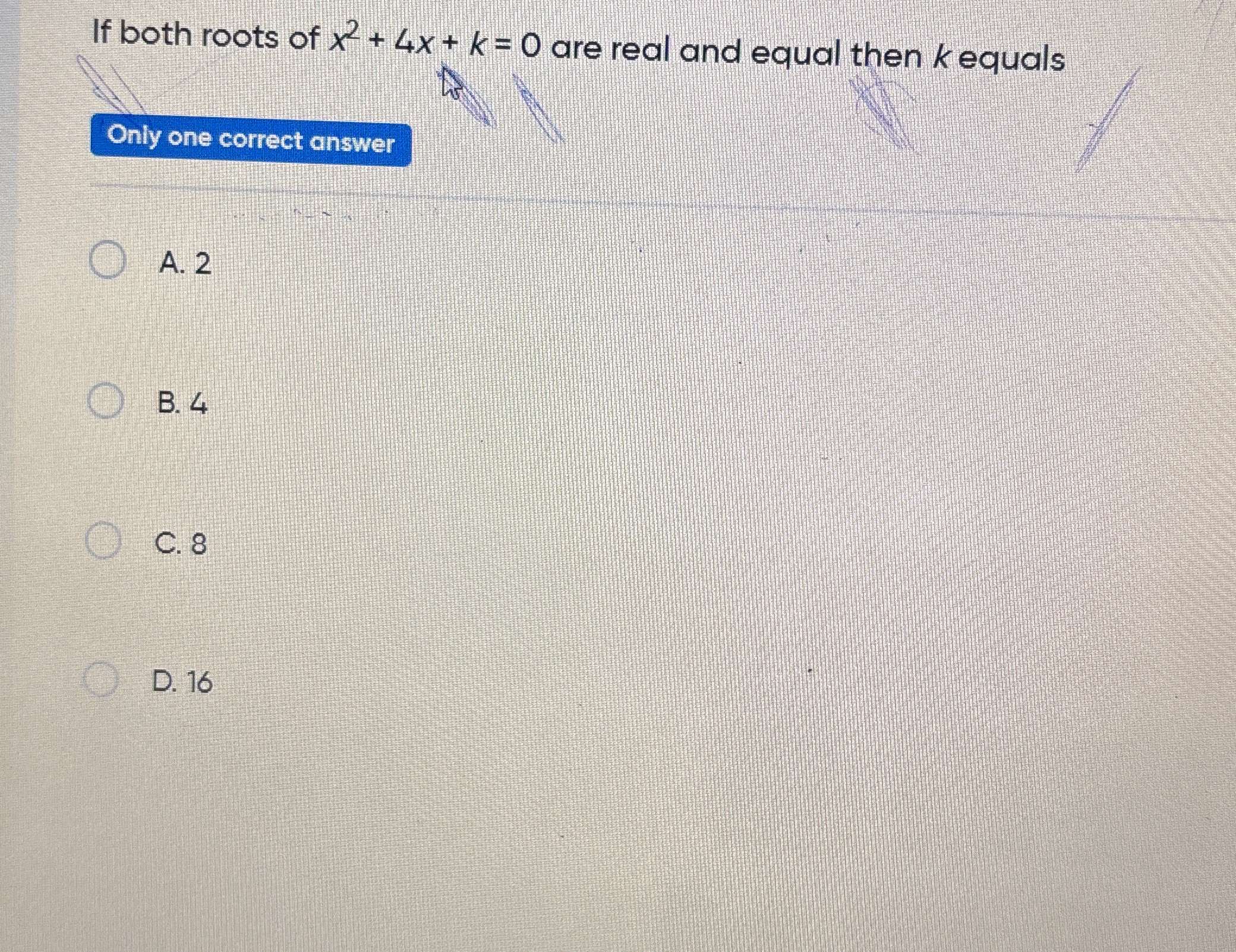
If both roots of x² + 4x + k = 0 are real and equal, then k equals?

Understand the Problem

The question asks for the value of k such that the quadratic equation x² + 4x + k has real and equal roots. This means we need to ensure that the discriminant (b² - 4ac) of the equation equals zero to find the correct value of k.

Answer

$k = 4$

Steps to Solve

Identify the coefficients In the quadratic equation $x^2 + 4x + k = 0$, the coefficients are:

$a = 1$ (coefficient of $x^2$)
$b = 4$ (coefficient of $x$)
$c = k$ (constant term)

Set up the discriminant condition For the roots to be real and equal, the discriminant ($D$) must equal zero. The discriminant formula is given by:
$$ D = b^2 - 4ac $$
Therefore, we set up the equation:
$$ 4^2 - 4(1)(k) = 0 $$
Simplify and solve for k Calculate $4^2$ and simplify the equation:
$$ 16 - 4k = 0 $$
Rearranging gives:
$$ 4k = 16 $$
Calculate the value of k Now, divide both sides by 4 to find $k$:
$$ k = \frac{16}{4} = 4 $$

The value of $k$ for which the equation has real and equal roots is $k = 4$.

More Information

The condition for a quadratic equation to have real and equal roots is determined by the discriminant being zero. In this case, when substituting $k = 4$, the roots will be equal.

Tips

Forgetting to set the discriminant equal to zero: Ensure that when looking for real and equal roots, the discriminant condition is properly applied.
Miscalculating the discriminant formula: Make sure to correctly apply values into the formula to avoid arithmetic mistakes.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!