If A = {x ∈ R: 4x² = 2x + 3} and B = {x ∈ R: log(x²) = (log(x))²}, find A ∩ B.
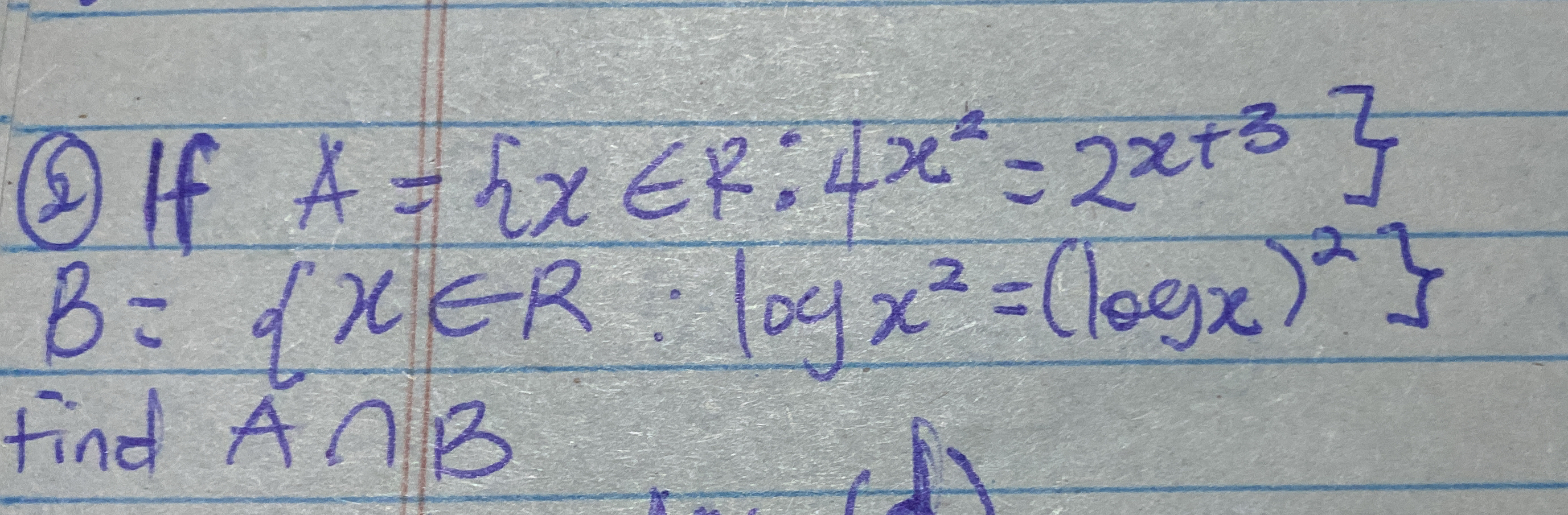
Understand the Problem
The question asks to find the intersection of two sets A and B where set A is defined by a polynomial equation and set B by a logarithmic function. The solution will involve determining the common elements in both sets.
Answer
The intersection is \( A \cap B = \{1\} \).
Answer for screen readers
The intersection ( A \cap B ) is: $$ A \cap B = {1} $$
Steps to Solve
- Define the sets A and B
Set ( A ) is defined by the polynomial equation ( 4x^2 = 2x + 3 ).
Set ( B ) is defined by the logarithmic equation ( \log x^2 = (\log x)^2 ).
- Solve for A
To solve for ( A ), rearrange the equation: $$ 4x^2 - 2x - 3 = 0 $$ Use the quadratic formula ( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ), where ( a = 4, b = -2, c = -3 ).
Calculate the discriminant: $$ D = (-2)^2 - 4(4)(-3) = 4 + 48 = 52 $$
Now use this to find: $$ x = \frac{2 \pm \sqrt{52}}{2 \cdot 4} = \frac{2 \pm 2\sqrt{13}}{8} = \frac{1 \pm \sqrt{13}}{4} $$ Thus, ( A = \left{ \frac{1 + \sqrt{13}}{4}, \frac{1 - \sqrt{13}}{4} \right} ).
- Solve for B
To solve for ( B ), we start with the logarithmic equation: $$ \log x^2 = (\log x)^2 $$ Setting ( y = \log x ), the equation becomes: $$ y^2 - 2y = 0 $$ Factoring gives: $$ y(y - 2) = 0 $$ Thus, ( y = 0 ) or ( y = 2 ). Converting back to ( x ):
- If ( y = 0 ): ( \log x = 0 ) implies ( x = 10^0 = 1 ).
- If ( y = 2 ): ( \log x = 2 ) implies ( x = 10^2 = 100 ).
So, ( B = {1, 100} ).
- Find the intersection A ∩ B
Now, we find the common elements between sets ( A ) and ( B ): $$ A \cap B = \left{ \frac{1 + \sqrt{13}}{4}, \frac{1 - \sqrt{13}}{4} \right} \cap {1, 100} $$
Calculating the values:
- ( \frac{1 + \sqrt{13}}{4} \approx 1.85 )
- ( \frac{1 - \sqrt{13}}{4} \approx -0.35 )
Only ( 1 ) is common to both sets.
The intersection ( A \cap B ) is: $$ A \cap B = {1} $$
More Information
The intersection of sets represents the elements that are common to both sets. In this instance, ( 1 ) is the only common value derived from both the polynomial and logarithmic equations.
Tips
- Failing to check if the solutions for ( A ) and ( B ) are valid by substituting back.
- Neglecting to consider the domain restrictions of logarithmic functions, which only allow positive values for ( x ).
AI-generated content may contain errors. Please verify critical information