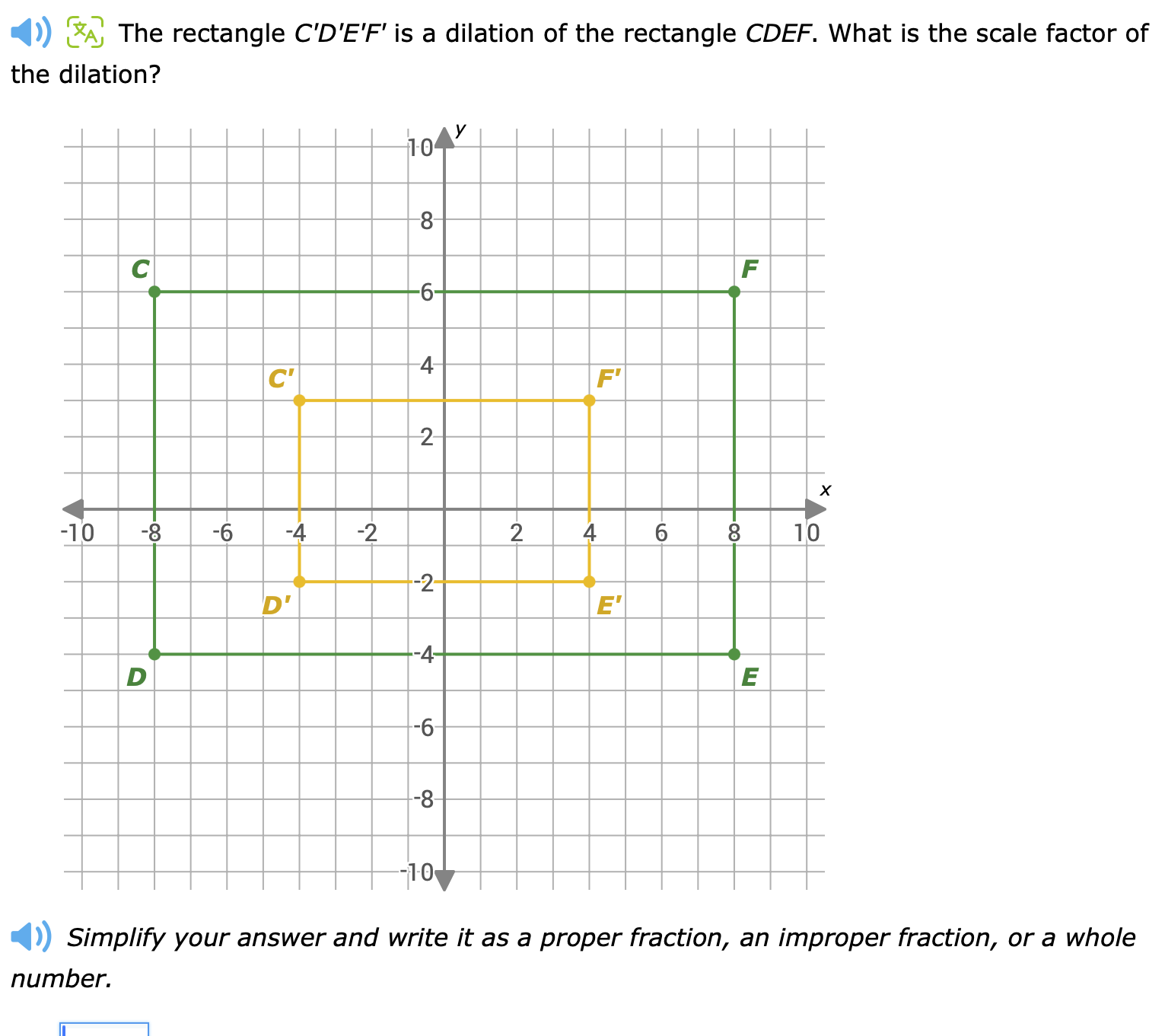
The rectangle C'D'E'F' is a dilation of the rectangle CDEF. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction,... The rectangle C'D'E'F' is a dilation of the rectangle CDEF. What is the scale factor of the dilation? Simplify your answer and write it as a proper fraction, an improper fraction, or a whole number. Read more

Steps to Solve

1. Identify the coordinates of the rectangles' vertices
   For rectangle CDEF, the coordinates of the vertices are:

• C(6, 6)
• D(-8, -4)
• E(8, -4)
• F(6, -8)

For rectangle C'D'E'F', the coordinates are:

• C'(-4, 4)
• D'(-4, -2)
• E'(4, -2)
• F'(4, 4)

2. Calculate the lengths of the corresponding sides
   Determine the lengths of one side for each rectangle. We can use the distance formula $d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$.

For side CD of rectangle CDEF: $$ CD = \sqrt{(6 - (-8))^2 + (6 - (-4))^2} = \sqrt{(6 + 8)^2 + (6 + 4)^2} = \sqrt{14^2 + 10^2} = \sqrt{196 + 100} = \sqrt{296} = 17.2 \text{ (approx)} $$

For side C'D' of rectangle C'D'E'F': $$ C'D' = \sqrt{(-4 - (-4))^2 + (4 - (-2))^2} = \sqrt{0^2 + (4 + 2)^2} = \sqrt{0 + 6^2} = 6 $$

3. Calculate the scale factor of dilation
   The scale factor $k$ can be found by taking the ratio of the lengths of corresponding sides: $$ k = \frac{\text{Length of corresponding side in smaller rectangle}}{\text{Length of corresponding side in larger rectangle}} = \frac{6}{17.2} $$

4. Simplify the ratio
   Perform the division: $$ k = \frac{6}{17.2} \approx 0.3488 $$
   For the purpose of simplification, we can leave this as a fraction if required.