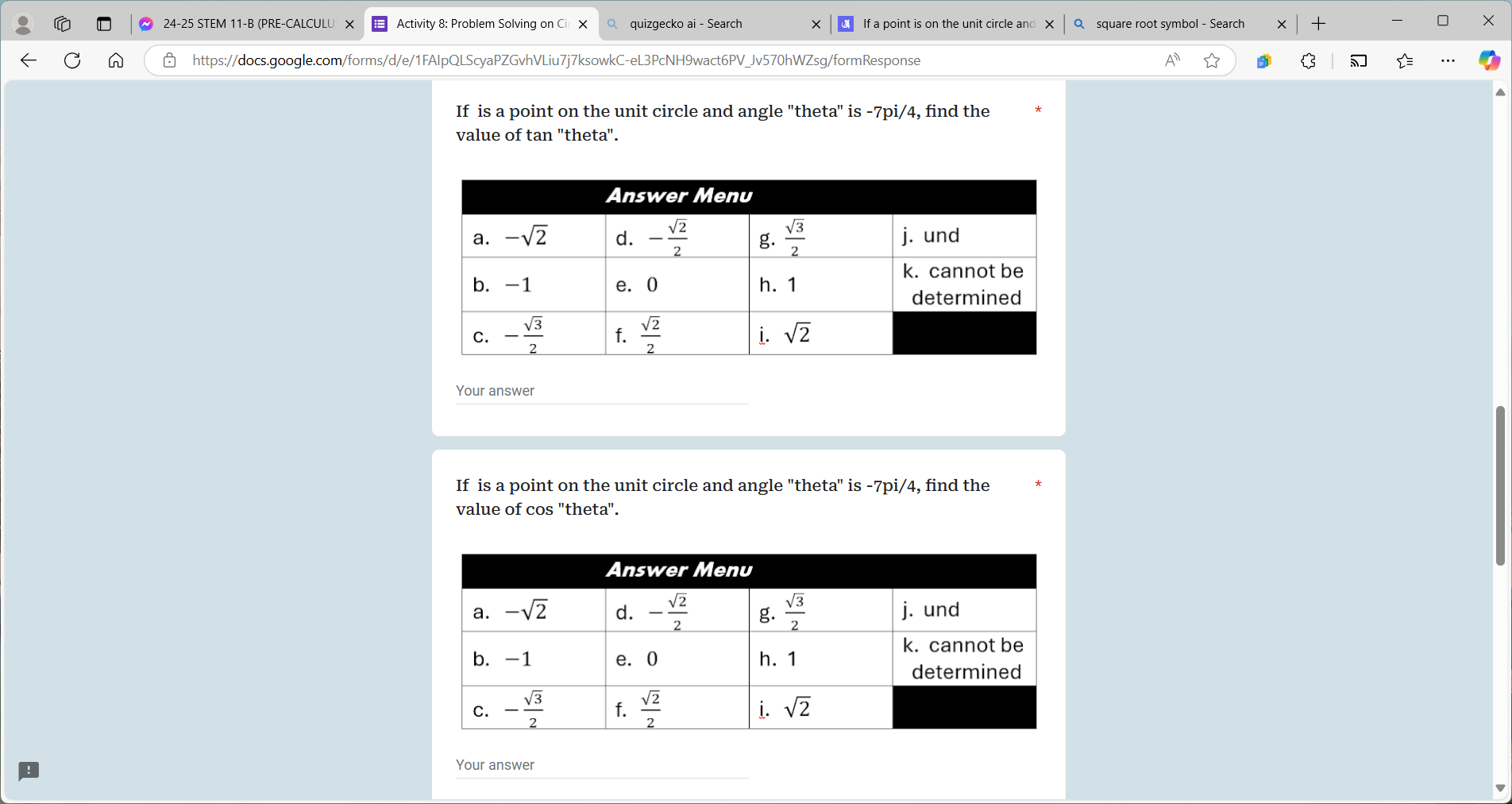
If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of tan 'theta'. If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of cos 'th... If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of tan 'theta'. If a point is on the unit circle and angle 'theta' is -7pi/4, find the value of cos 'theta'.
Understand the Problem
The question is asking us to find the values of tangent and cosine for a point on the unit circle at the angle -7pi/4. We will use the properties of the unit circle and trigonometric functions to determine these values.
Answer
- $\tan\left(-\frac{7\pi}{4}\right) = 1$ and $\cos\left(-\frac{7\pi}{4}\right) = \frac{\sqrt{2}}{2}$
Answer for screen readers
- The value of $\tan\left(-\frac{7\pi}{4}\right)$ is 1.
- The value of $\cos\left(-\frac{7\pi}{4}\right)$ is $\frac{\sqrt{2}}{2}$.
Steps to Solve
- Determine the equivalent positive angle To find the equivalent angle of $-\frac{7\pi}{4}$ that lies between $0$ and $2\pi$, add $2\pi$ (which is equivalent to $\frac{8\pi}{4}$).
$$ -\frac{7\pi}{4} + 2\pi = -\frac{7\pi}{4} + \frac{8\pi}{4} = \frac{\pi}{4} $$
-
Identify the coordinates on the unit circle The angle $\frac{\pi}{4}$ corresponds to the coordinates on the unit circle, which are: $$ \left(\cos\left(\frac{\pi}{4}\right), \sin\left(\frac{\pi}{4}\right)\right) = \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right) $$
-
Calculate the values of tangent and cosine The tangent and cosine values can now be calculated.
-
The value of tangent is given by: $$ \tan\left(\theta\right) = \frac{\sin\left(\theta\right)}{\cos\left(\theta\right)} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 $$
-
The value of cosine is: $$ \cos\left(-\frac{7\pi}{4}\right) = \frac{\sqrt{2}}{2} $$
- The value of $\tan\left(-\frac{7\pi}{4}\right)$ is 1.
- The value of $\cos\left(-\frac{7\pi}{4}\right)$ is $\frac{\sqrt{2}}{2}$.
More Information
Both values are derived from the properties of the unit circle, where the coordinates corresponding to $\frac{\pi}{4}$ give us direct values for sine and cosine, leading to the tangent.
Tips
- Mistakenly adding or subtracting angles incorrectly when finding equivalent angles.
- Confusing the coordinates of angles in different quadrants, which could lead to incorrect sine or cosine values.
AI-generated content may contain errors. Please verify critical information