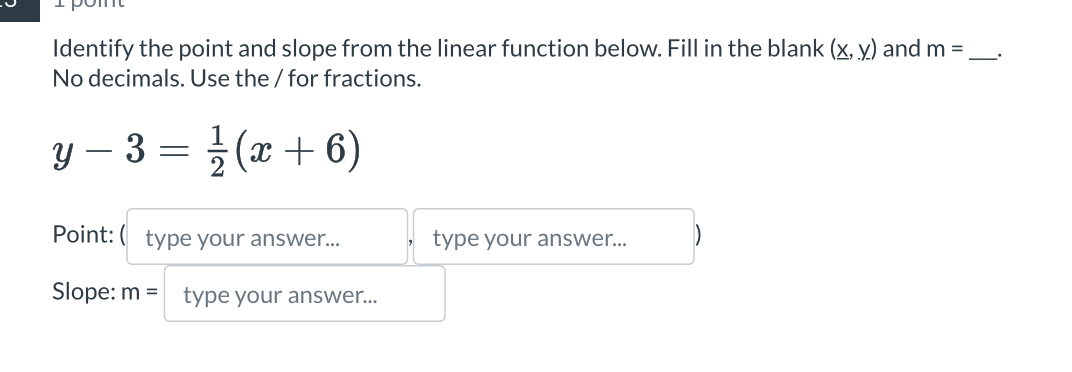
Identify the point and slope from the linear function below. Fill in the blank (x, y) and m = __. No decimals. Use the / for fractions.
Understand the Problem
The question is asking us to identify a point and the slope from a given linear equation in point-slope form. We need to extract the values of (x, y) and m from the equation and fill in the blanks accordingly.
Answer
Point: \((-6, 3)\), Slope: \(m = \frac{1}{2}\)
Answer for screen readers
Point: ((-6, 3))
Slope: (m = \frac{1}{2})
Steps to Solve
- Identify the point from the equation
The equation is in point-slope form: $y - y_1 = m(x - x_1)$.
From the equation $y - 3 = \frac{1}{2}(x + 6)$, we can see that:
- $y_1 = 3$
- The term $(x + 6)$ implies that $x_1 = -6$ (since it can be rewritten as $x - (-6)$).
Thus, the point is ((-6, 3)).
- Determine the slope
The slope (m) is represented as the coefficient of the $(x-x_1)$ term in the point-slope form. Here, we have (m = \frac{1}{2}) directly from the equation.
- Compile the results
Based on the above calculations, our results are:
- Point: ((-6, 3))
- Slope: (m = \frac{1}{2})
Point: ((-6, 3))
Slope: (m = \frac{1}{2})
More Information
The point-slope form of a linear equation is useful for translating points and slopes into various forms of linear equations. It is particularly helpful for graphing lines or identifying relationships in linear functions.
Tips
- Misidentifying the slope from the equation. Make sure to focus on the coefficient attached to ( (x - x_1) ).
- Confusing the signs when determining the point values, especially with the transformation from ( (x + 6) ) to ( x - (-6) ).
AI-generated content may contain errors. Please verify critical information