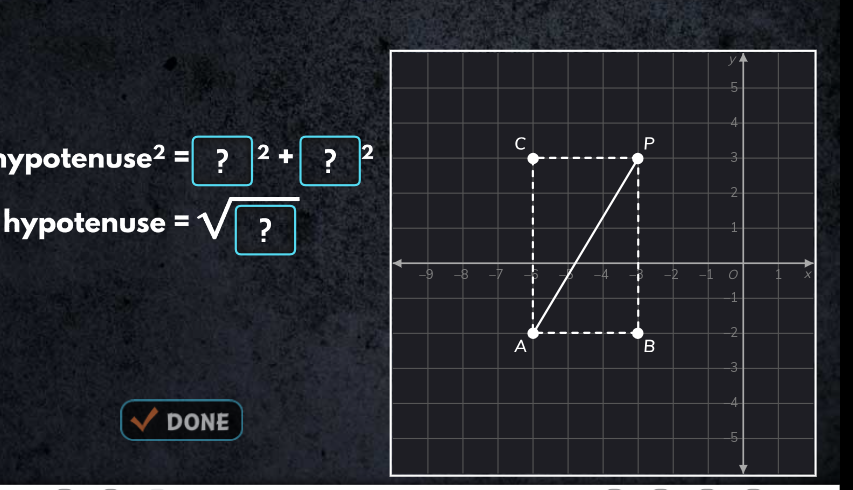
hypotenuse² = ?² + ?²; hypotenuse = √(?)
Understand the Problem
The question is asking to find the lengths of the sides of a right triangle using the Pythagorean theorem. We need to determine the values represented by the question marks for the calculation of the hypotenuse.
Answer
The lengths of the sides are \(2\) and \(3\), and the hypotenuse is \(\sqrt{13}\).
Answer for screen readers
The lengths of the sides are (2) and (3), with the hypotenuse being (\sqrt{13}).
Steps to Solve
-
Identify the Coordinates of Points The vertices of the right triangle are given as points A, B, and P on the Cartesian plane. The coordinates are:
- A: (-8, 0)
- B: (-8, 2)
- P: (-5, 2)
-
Calculate the Lengths of the Triangle's Legs We can use the distance formula to find the lengths of sides AB and AP.
The length of side AB (vertical leg): [ AB = |y_B - y_A| = |2 - 0| = 2 ]
The length of side AP (horizontal leg): [ AP = |x_P - x_A| = |-5 - (-8)| = |-5 + 8| = 3 ]
-
Apply the Pythagorean Theorem According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides: [ \text{hypotenuse}^2 = AB^2 + AP^2 ] Substituting the values we found: [ \text{hypotenuse}^2 = 2^2 + 3^2 ]
-
Calculate the Hypotenuse Length First, compute the squared values: [ 2^2 = 4 \quad \text{and} \quad 3^2 = 9 ] Now add them together: [ \text{hypotenuse}^2 = 4 + 9 = 13 ] Finally, take the square root to find the hypotenuse: [ \text{hypotenuse} = \sqrt{13} ]
The lengths of the sides are (2) and (3), with the hypotenuse being (\sqrt{13}).
More Information
The Pythagorean theorem is fundamental in geometry, relating the lengths of the sides of right triangles. The lengths can represent various real-world scenarios, such as distances in navigation or construction.
Tips
- Forgetting to square the side lengths: Ensure both sides are squared before adding.
- Mistaking the triangle configuration: Confirm points A, B, and P indeed form a right triangle.
- Calculating absolute lengths incorrectly: Carefully apply the distance formula to avoid errors.
AI-generated content may contain errors. Please verify critical information