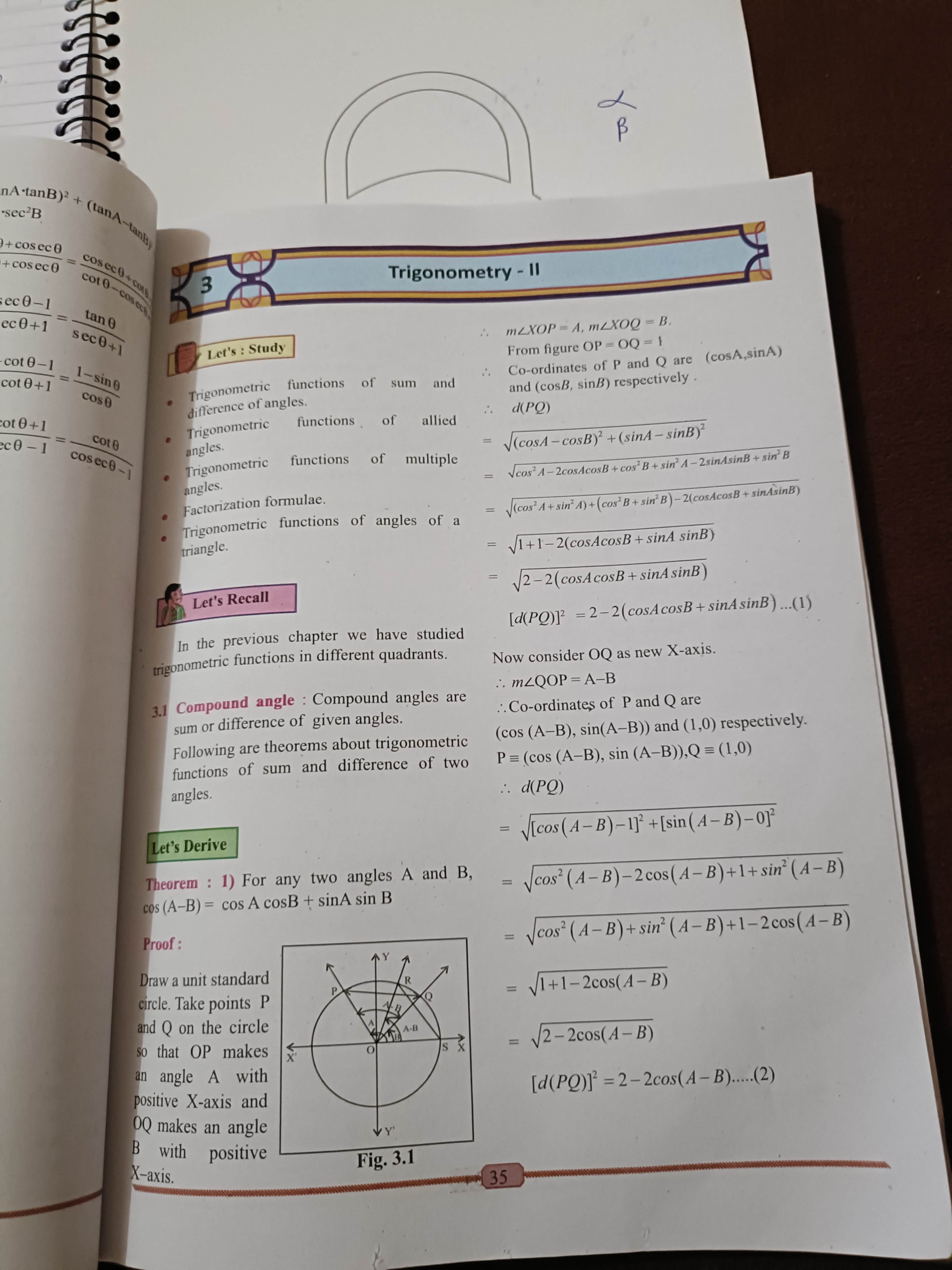
How to derive the formula for the distance between points P and Q in terms of angles A and B?

Steps to Solve

1. Understanding Coordinates of Points P and Q

   In the unit circle, the coordinates of point P corresponding to angle A are given by $(\cos A, \sin A)$ and for angle B by $(\cos B, \sin B)$.

2. Calculating the Distance d(P, Q)

   The distance between points P and Q is calculated using the distance formula: $$ d(PQ) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$ Substituting in the coordinates of P and Q: $$ d(PQ) = \sqrt{(\cos B - \cos A)^2 + (\sin B - \sin A)^2} $$

3. Expanding the Distance Formula

   Expanding the squared terms, we have: $$ d(PQ) = \sqrt{(\cos^2 B - 2\cos A \cos B + \cos^2 A) + (\sin^2 B - 2\sin A \sin B + \sin^2 A)} $$ Using the identity $\sin^2 x + \cos^2 x = 1$: $$ d(PQ) = \sqrt{2 - 2(\cos A \cos B + \sin A \sin B)} $$

4. Using the Cosine of the Angle Difference

   Recognizing that the expression $\cos A \cos B + \sin A \sin B$ can be simplified as: $$ \cos(A - B) $$ Thus, we rewrite the distance as: $$ d(PQ) = \sqrt{2 - 2\cos(A - B)} $$

5. Final Simplification

   By factoring out 2, we can further simplify: $$ d(PQ) = \sqrt{2(1 - \cos(A - B))} = \sqrt{2 \cdot 2 \sin^2\left(\frac{A - B}{2}\right)} = 2\sin\left(\frac{A - B}{2}\right) $$