f(x) = √(x - 2) + 1
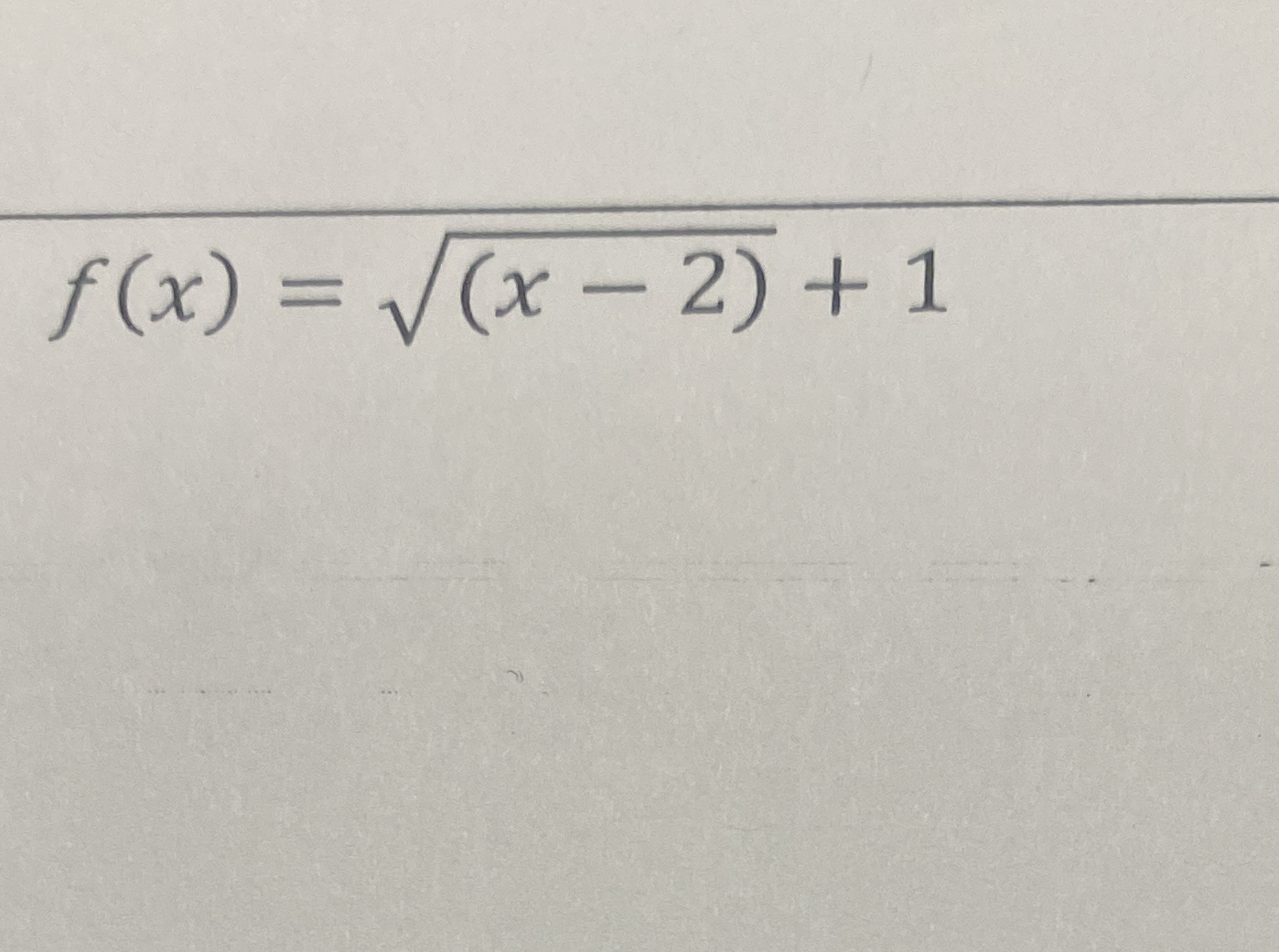
Understand the Problem
The question involves a mathematical function defined as f(x) = √(x - 2) + 1 and may require analysis, such as finding its domain, range, or graphing it.
Answer
Domain: $[2, \infty)$; Range: $[1, \infty)$
Answer for screen readers
Domain: $[2, \infty)$
Range: $[1, \infty)$
Steps to Solve
- Determine the Domain of f(x)
The function $f(x) = \sqrt{x - 2} + 1$ involves a square root, which requires the expression inside the square root to be non-negative.
So, we set up the inequality:
$$ x - 2 \geq 0 $$
Solving this gives:
$$ x \geq 2 $$
Thus, the domain of $f(x)$ is $[2, \infty)$.
- Determine the Range of f(x)
Next, we analyze the output of the function. The minimum value occurs when $x = 2$:
$$ f(2) = \sqrt{2 - 2} + 1 = 0 + 1 = 1 $$
As $x$ increases, the square root increases, so $f(x)$ approaches infinity.
Thus, the range of $f(x)$ is $[1, \infty)$.
- Graphing the Function
To graph $f(x)$, we note that the function has a starting point at (2, 1) and increases without bound. The graph will look like a curve that starts at the point (2, 1) and rises to the right.
- Summary of Function Behavior
The function is defined for $x \geq 2$, starting from $f(x) = 1$ and goes upwards indefinitely.
Domain: $[2, \infty)$
Range: $[1, \infty)$
More Information
The function is a transformation of the basic square root function, which shifts it upward by 1 unit. Understanding the domain and range is crucial for analyzing functions, especially those involving square roots.
Tips
- Forgetting to set the expression inside the square root to be non-negative when determining the domain.
- Miscalculating the starting value of the function at its domain's boundary.
AI-generated content may contain errors. Please verify critical information