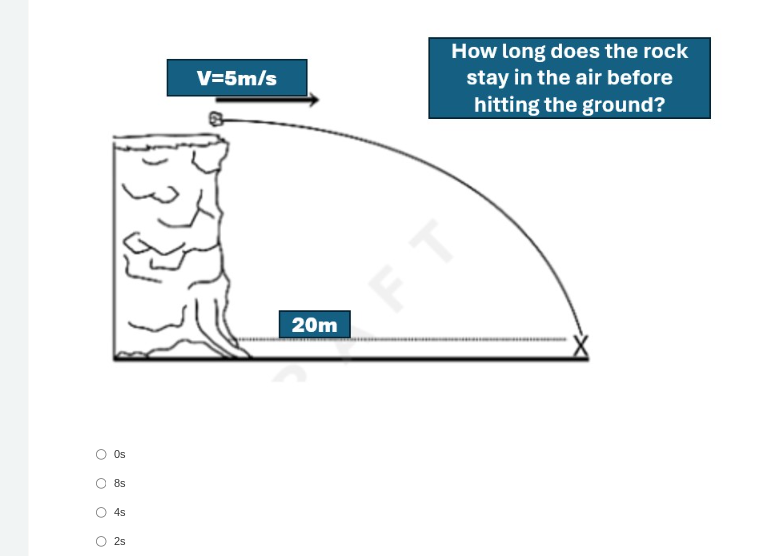
How long does the rock stay in the air before hitting the ground?
Understand the Problem
The question is asking for the time it takes for a rock to hit the ground after being projected horizontally from a height of 20 meters. This involves calculating the time of free fall due to gravity, not the horizontal velocity.
Answer
The rock stays in the air for approximately $2.02$ seconds.
Answer for screen readers
The time it takes for the rock to hit the ground is approximately ( 2.02 ) seconds.
Steps to Solve
-
Identify the formula for free fall To find the time it takes for an object to fall from a height under the influence of gravity, we can use the formula: $$ h = \frac{1}{2}gt^2 $$ where ( h ) is the height (20 m), ( g ) is the acceleration due to gravity (approximately ( 9.81 , \text{m/s}^2 )), and ( t ) is the time in seconds.
-
Rearrange the formula to solve for time ( t ) We need to solve the formula for ( t ): $$ t = \sqrt{\frac{2h}{g}} $$
-
Substitute the values into the formula Substituting ( h = 20 , \text{m} ) and ( g = 9.81 , \text{m/s}^2 ): $$ t = \sqrt{\frac{2 \cdot 20}{9.81}} $$
-
Calculate the value Now we calculate ( t ): $$ t = \sqrt{\frac{40}{9.81}} \approx \sqrt{4.08} \approx 2.02 , \text{s} $$
The time it takes for the rock to hit the ground is approximately ( 2.02 ) seconds.
More Information
The calculation assumes no air resistance and that the only force acting on the rock during its fall is gravity. In real-world scenarios, factors like air resistance might slightly affect the fall time but are often negligible for such cases.
Tips
- Confusing horizontal and vertical motion: This problem focuses solely on the vertical drop, ignoring any horizontal velocity.
- Not accounting for the correct units for ( g ): Ensure you're using ( 9.81 , \text{m/s}^2 ) for gravity in calculations.
AI-generated content may contain errors. Please verify critical information