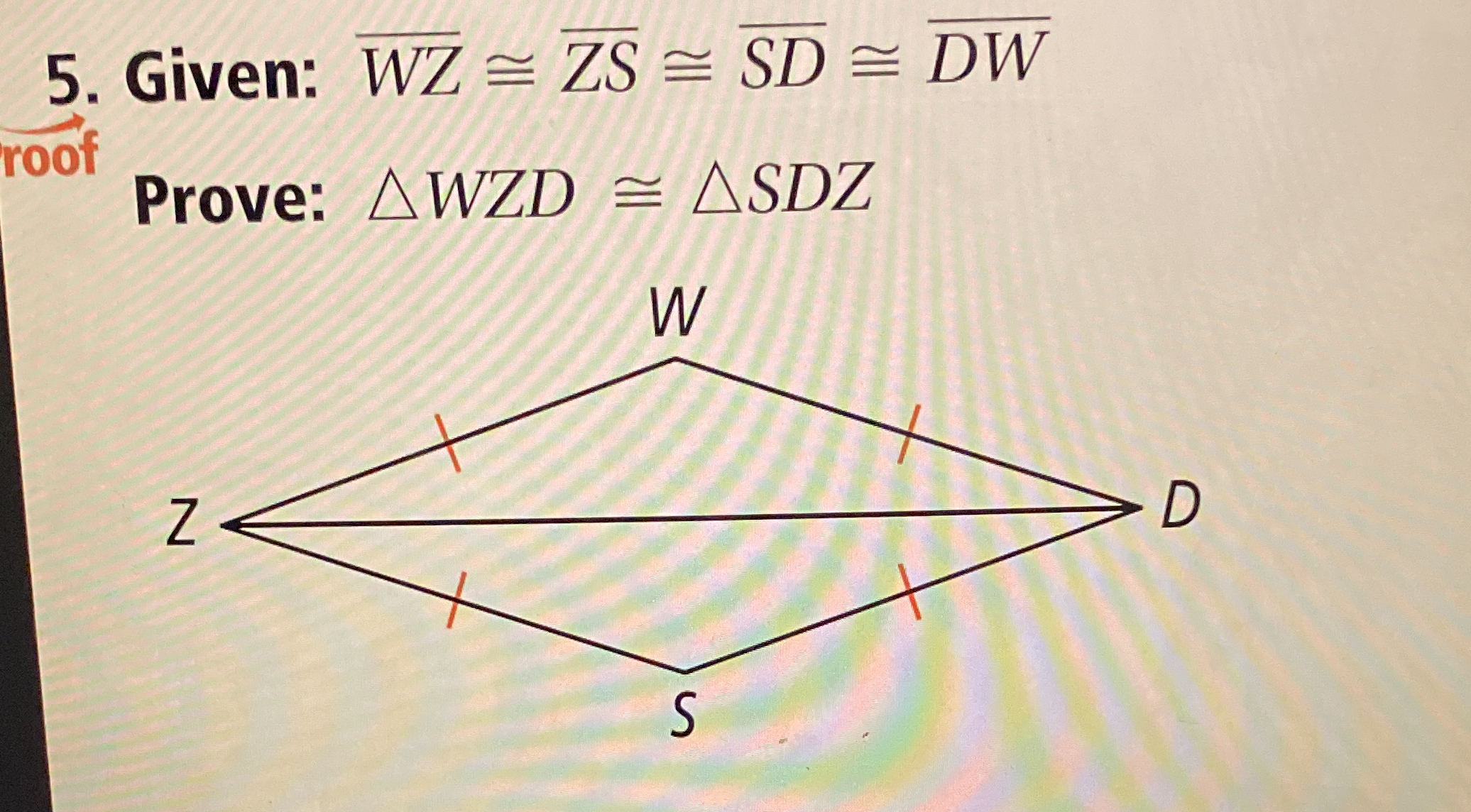
Given: WZ ≅ ZS ≅ SD ≅ DW. Prove: ∆WZD ≅ ∆SDZ.
Understand the Problem
The question is asking to prove the congruence of two triangles, ∆WZD and ∆SDZ, given that the side lengths WZ, ZS, SD, and DW are all equal. This involves using the properties of triangles and possibly the congruence postulates.
Answer
$$ \triangle WZD \cong \triangle SDZ $$
Answer for screen readers
$$ \triangle WZD \cong \triangle SDZ $$
Steps to Solve
-
Identify Given Information The problem gives us that $WZ \cong ZS \cong SD \cong DW$. This means that all four sides are of equal length.
-
Identify Corresponding Sides Recognize that triangles $\triangle WZD$ and $\triangle SDZ$ share the side $DZ$ and both have equal sides from the given information. Therefore, we have:
- $WZ \cong SD$ (from the given)
- $DZ \cong DZ$ (common side)
- $ZS \cong ZS$ (also from the given)
-
Apply the Side-Side-Side (SSS) Congruence Postulate According to the SSS Congruence Postulate, if three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent. Hence, we can establish: $$ \triangle WZD \cong \triangle SDZ $$
-
Conclude with Proved Congruence Since we've shown that all three sides of $\triangle WZD$ are congruent to the three sides of $\triangle SDZ$, we conclude that: $$ \triangle WZD \cong \triangle SDZ $$
$$ \triangle WZD \cong \triangle SDZ $$
More Information
This proof employs the Side-Side-Side (SSS) postulate, which is foundational in proving triangle congruence. The fact that all given side lengths are equal ensures that the two triangles are congruent.
Tips
- Ignoring Common Sides: Failing to recognize a shared side can lead to incorrect applications of congruence criteria.
- Assuming Angles are Equal: It's crucial to rely on side lengths for SSS; using angle measures incorrectly can lead to errors.
AI-generated content may contain errors. Please verify critical information