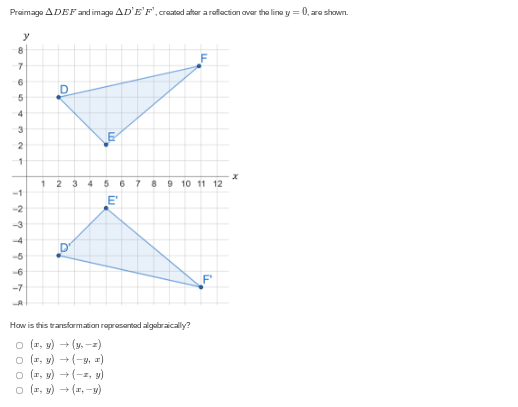
How is this transformation represented algebraically?
Understand the Problem
The question is asking how the transformation of the given geometric figure, as shown in the image, can be represented mathematically. It specifically involves identifying the correct algebraic representation for a reflection over the line y = 0.
Answer
The transformation is represented as $(x, y) \to (x, -y)$.
Answer for screen readers
The correct algebraic representation for the transformation is $(x, y) \to (x, -y)$.
Steps to Solve
-
Identify the Transformation The transformation described is a reflection over the line $y = 0$. This means every point's $y$-coordinate will change sign, while the $x$-coordinate remains the same.
-
Define the Reflection Rule The rule for reflecting a point $(x, y)$ over the line $y = 0$ can be expressed mathematically as: $$(x, y) \to (x, -y)$$
-
Conclusion Based on the transformation, the points of triangle $\Delta DEF$ reflect to $\Delta D'E'F'$ by maintaining their $x$-coordinates and negating their $y$-coordinates.
The correct algebraic representation for the transformation is $(x, y) \to (x, -y)$.
More Information
This transformation indicates that any point $(x, y)$ will be reflected to $(x, -y}$ across the line $y = 0$. This is a common type of geometric transformation involving reflections across horizontal lines.
Tips
- Confusing the reflection over the line $y=0$ with a reflection over the line $x=0$, which would yield a different rule, $(x,y) \to (-x,y)$.
- Misunderstanding that only the $y$-coordinate changes; the $x$-coordinate remains unchanged during a reflection over the line $y=0$.
AI-generated content may contain errors. Please verify critical information