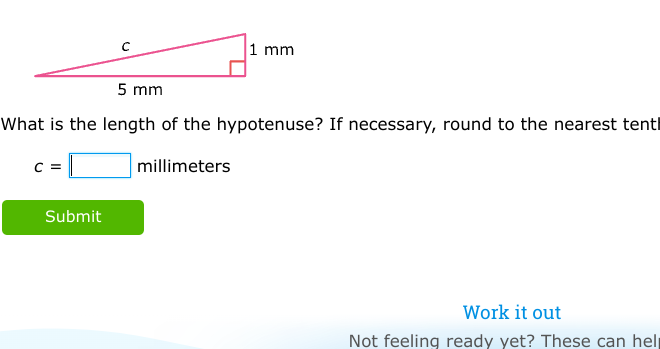
What is the length of the hypotenuse? If necessary, round to the nearest tenth of a millimeter.
Understand the Problem
The question is asking for the length of the hypotenuse of a right triangle given the lengths of the other two sides, which are 1 mm and 5 mm. We will use the Pythagorean theorem to find the hypotenuse.
Answer
The length of the hypotenuse is approximately $5.1$ mm.
Answer for screen readers
The length of the hypotenuse is approximately $5.1$ mm.
Steps to Solve
- Identify the lengths of the sides
The lengths of the two sides of the right triangle are given as 1 mm and 5 mm. Let these be denoted as:
- One side ( a = 1 ) mm
- Other side ( b = 5 ) mm
-
Apply the Pythagorean theorem
The Pythagorean theorem states that for a right triangle:
$$ c^2 = a^2 + b^2 $$
where ( c ) is the length of the hypotenuse. -
Substitute the values into the equation
We can plug in the values of ( a ) and ( b ) into the equation:
$$ c^2 = (1 , \text{mm})^2 + (5 , \text{mm})^2 $$
Calculating this gives:
$$ c^2 = 1 + 25 $$
$$ c^2 = 26 $$ -
Calculate the length of the hypotenuse
To find ( c ), we need to take the square root of 26:
$$ c = \sqrt{26} $$
Using a calculator, we find:
$$ c \approx 5.099 $$ -
Round to the nearest tenth
Rounding 5.099 to the nearest tenth gives:
$$ c \approx 5.1 , \text{mm} $$
The length of the hypotenuse is approximately $5.1$ mm.
More Information
The hypotenuse is the longest side of a right triangle, and it can be calculated using the Pythagorean theorem. This theorem is a fundamental principle in geometry and is widely used in various fields including architecture, engineering, and physics.
Tips
- Mixing up which sides to square; always ensure to square the two shorter sides.
- Incorrectly calculating the square root. Be careful with the use of calculators and rounding.
AI-generated content may contain errors. Please verify critical information