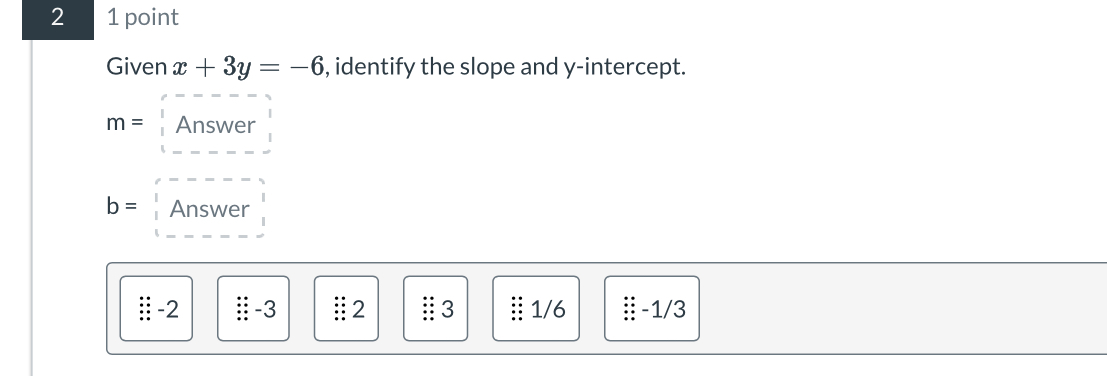
Given x + 3y = -6, identify the slope and y-intercept.

Understand the Problem

The question is asking us to identify the slope (m) and y-intercept (b) of the linear equation given in the form x + 3y = -6. To solve it, we will rearrange the equation into the slope-intercept form (y = mx + b).

Answer

Slope $ m = -\frac{1}{3} $, Y-intercept $ b = -2 $

Steps to Solve

Rearranging the equation

We start with the equation ( x + 3y = -6 ). To put it in slope-intercept form ( y = mx + b ), we need to isolate ( y ).

Isolate ( 3y )

Subtract ( x ) from both sides: $$ 3y = -x - 6 $$

Divide by 3

Now, divide every term by 3 to isolate ( y ): $$ y = -\frac{1}{3}x - 2 $$

Identify the slope and y-intercept

From the equation ( y = mx + b ), we can identify the slope ( m ) and the y-intercept ( b ):

The slope ( m = -\frac{1}{3} )
The y-intercept ( b = -2 )

Slope ( m = -\frac{1}{3} )

Y-intercept ( b = -2 )

More Information

In slope-intercept form ( y = mx + b ), ( m ) represents the slope of the line, which indicates the steepness and direction, while ( b ) represents the point where the line crosses the y-axis. Here, the line slopes downwards as ( m ) is negative.

Tips

Forgetting to properly isolate ( y ) can lead to an incorrect slope or y-intercept.
Confusion about the signs during rearrangement can also lead to errors in identifying ( m ) and ( b ).

Thank you for voting!