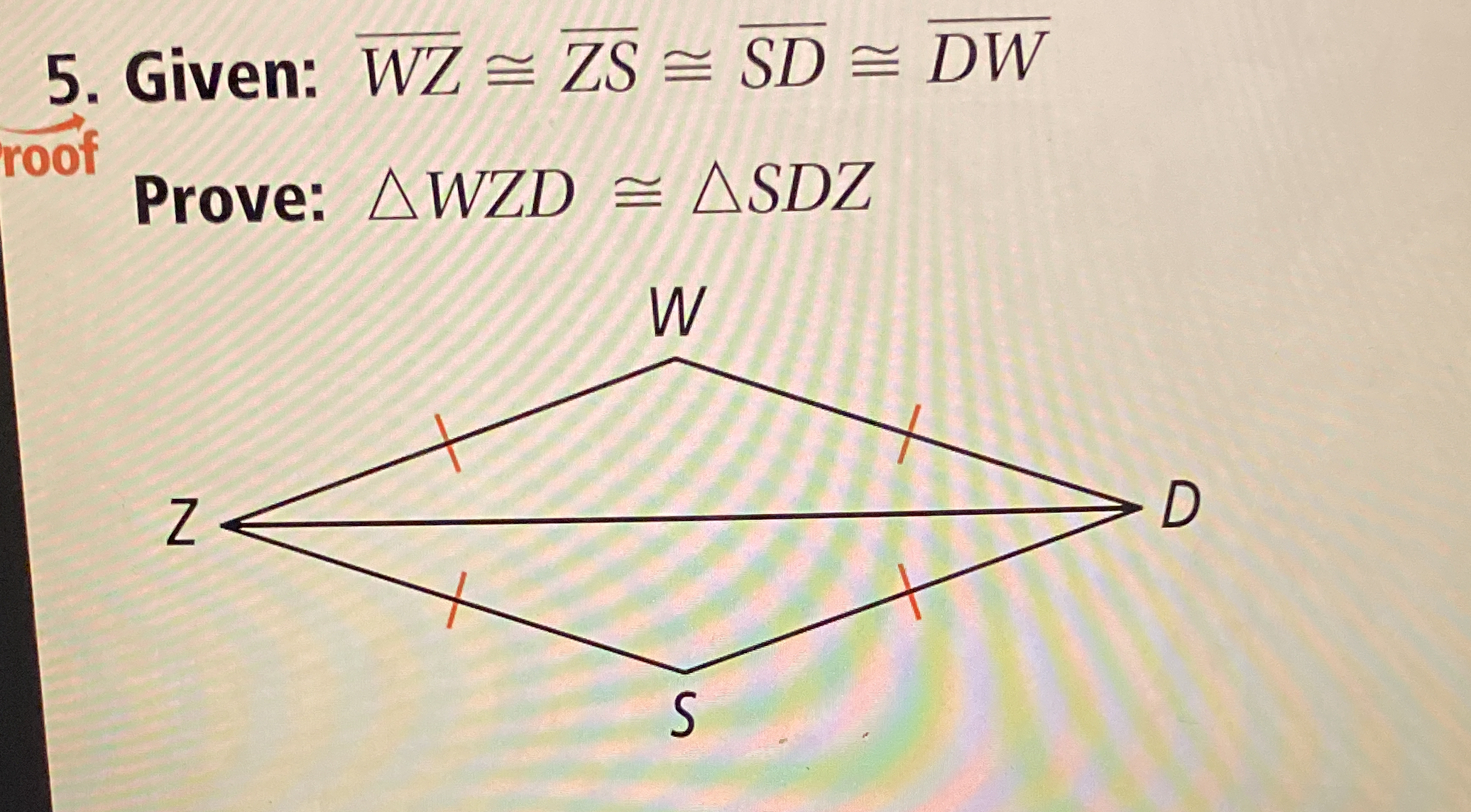
Given: WZ ≅ ZS ≅ SD ≅ DW. Prove: ΔWZD ≅ ΔSDZ.
Understand the Problem
The question presents a geometric proof involving congruent segments and triangles. It asks to prove that triangle WZD is congruent to triangle SDZ based on the given congruent segments.
Answer
$$ \triangle WZD \cong \triangle SDZ $$
Answer for screen readers
$$ \triangle WZD \cong \triangle SDZ $$
Steps to Solve
- List the Given Information We have the following congruent segments:
- $WZ \cong ZS$
- $ZS \cong SD$
- $SD \cong DW$
-
Identify the Shared Side Both triangles $\triangle WZD$ and $\triangle SDZ$ share the segment $ZD$.
-
Apply the Property of Congruence From the given, we know:
- $WZ \cong ZS$
- $ZS \cong SD$
- Thus, $WZ \cong SD$
- Conclude Triangle Congruence We have established:
- $WZ \cong SD$
- $ZD$ is shared (common side)
- $ZS \cong ZS$ (reflexive property)
This leads to: $$ \triangle WZD \cong \triangle SDZ $$ by the Side-Side-Side (SSS) congruence theorem.
$$ \triangle WZD \cong \triangle SDZ $$
More Information
The triangle congruence is based on the SSS criterion, where all three sides of one triangle are equal to the corresponding sides of another triangle. This ensures that the two triangles are congruent in shape and size.
Tips
- Misidentifying the Shared Side: A common mistake is not recognizing that $ZD$ is the shared side between the two triangles. Always check for a shared side when proving triangle congruence.
- Forgetting Properties of Congruence: Ensure that you don't overlook any congruent sides as given, which can mislead the proof.
AI-generated content may contain errors. Please verify critical information