Given v = (3, -6) and u · v = 33, find the vector u.
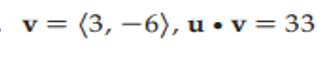
Understand the Problem
The question is asking to find a vector 'u' such that its dot product with vector 'v' equals 33, given that 'v' is (3, -6). This involves applying the dot product formula.
Answer
The vector $\mathbf{u} = \langle 11, 0 \rangle$.
Answer for screen readers
The vector $\mathbf{u} = \langle 11, 0 \rangle$ satisfies the condition $\mathbf{u} \cdot \mathbf{v} = 33$.
Steps to Solve
- Understand the Dot Product Formula
The dot product of two vectors $\mathbf{u} = \langle u_1, u_2 \rangle$ and $\mathbf{v} = \langle 3, -6 \rangle$ is calculated as:
$$\mathbf{u} \cdot \mathbf{v} = u_1 \cdot 3 + u_2 \cdot (-6)$$
We know that this dot product should equal 33:
$$u_1 \cdot 3 + u_2 \cdot (-6) = 33$$
- Set up the Equation
From the above, we can set up the equation:
$$3u_1 - 6u_2 = 33$$
- Rearrange and Simplify the Equation
To simplify, divide the entire equation by 3:
$$u_1 - 2u_2 = 11$$
This equation represents a line in the $u_1$-$u_2$ plane.
- Express One Variable in Terms of the Other
Let’s express $u_1$ in terms of $u_2$:
$$u_1 = 11 + 2u_2$$
This allows us to find various solutions for $\mathbf{u}$ based on the choice of $u_2$.
- Select a Value for $u_2$
We can choose any value for $u_2$. For example, if we let $u_2 = 0$:
$$u_1 = 11 + 2(0) = 11$$
So one possible solution for $\mathbf{u}$ is $\mathbf{u} = \langle 11, 0 \rangle$.
- Verify the Solution
To verify, calculate the dot product:
$$\mathbf{u} \cdot \mathbf{v} = 11 \cdot 3 + 0 \cdot (-6) = 33$$
This satisfies the condition given in the problem.
The vector $\mathbf{u} = \langle 11, 0 \rangle$ satisfies the condition $\mathbf{u} \cdot \mathbf{v} = 33$.
More Information
The solution $u_2 = 0$ gives one particular vector. Any other value for $u_2$ will yield a different vector, all of which are on the line defined by the equation $u_1 - 2u_2 = 11$.
Tips
- Assuming there is only one solution: The dot product equation yields a line of solutions for $\mathbf{u}$, not just a single vector.
- Miscalculating the dot product: Double-check arithmetic when substituting back to verify solutions.
AI-generated content may contain errors. Please verify critical information