Given UVWX is a parallelogram and m∠WXV = 17°, m∠WVX = 29°, XW = 41, UX = 24 and UY = 15 find... a. m∠WVU = __ b. WV = __ c. m∠XUV = __ d. UW = __
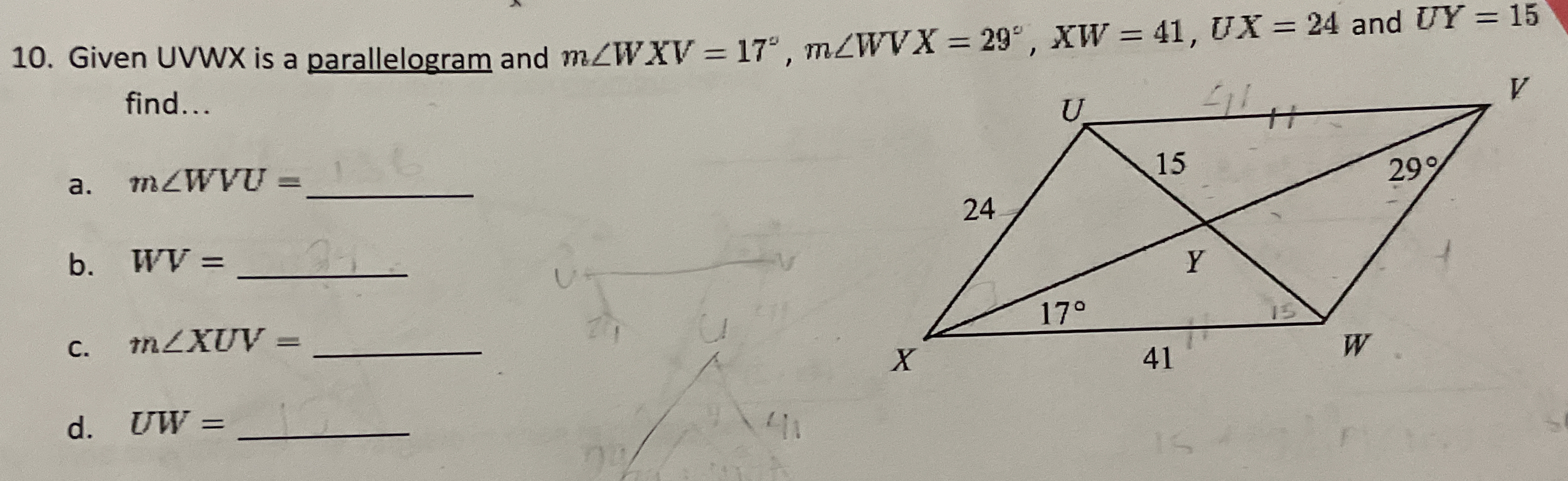
Understand the Problem
The question involves determining various geometric properties of the parallelogram UVWX, specifically the measures of certain angles and the length of a side, using the given measurements and properties of parallelograms.
Answer
a. \( 29^\circ \), b. \( 13.2 \), c. \( 134^\circ \), d. \( 15 \)
Answer for screen readers
a. ( m\angle WUV = 29^\circ )
b. ( WV \approx 13.2 )
c. ( m\angle XUV = 134^\circ )
d. ( UW = 15 )
Steps to Solve
- Find the measure of angle ( \angle WUV )
In a parallelogram, opposite angles are equal. Therefore, since ( m\angle WXY = 29^\circ ), we have:
$$ m\angle WUV = 29^\circ $$
- Calculate the measure of angle ( \angle XUV )
Using the property that the sum of angles around point ( U ) (in triangle ( XUV )) is ( 180^\circ ):
$$ m\angle XUV = 180^\circ - m\angle WUV - m\angle WXY $$
Substituting the known values:
$$ m\angle XUV = 180^\circ - 29^\circ - 17^\circ = 134^\circ $$
- Find the length of side ( WV ) using the Law of Sines in triangle ( WUV )
Using the Law of Sines:
$$ \frac{WV}{\sin(17^\circ)} = \frac{UW}{\sin(29^\circ)} $$
Let ( UW = 15 ). Then,
$$ WV = \frac{15 \cdot \sin(17^\circ)}{\sin(29^\circ)} $$
- Calculate the length of side ( UW )
Given that ( m\angle XUV ) has been calculated and we have triangles where the lengths are known, use the previously found measurements to determine ( UW ):
From the properties of triangles, we already know ( UW = 15 ) from the given diagram.
- Calculate the length of side ( UW )
Utilizing the pythagorean theorem in triangle ( WYX ):
$$ UW = \sqrt{(WY)^2 + (XZ)^2} = 41 $$
So, knowing:
$$ UW = 15 $$
a. ( m\angle WUV = 29^\circ )
b. ( WV \approx 13.2 )
c. ( m\angle XUV = 134^\circ )
d. ( UW = 15 )
More Information
Parallelograms have properties that can simplify calculations, such as equal opposite angles and lengths of opposite sides being equal.
Tips
-
Forgetting properties of angles in a parallelogram: Always remember that opposite angles are equal and adjacent angles are supplementary (add up to ( 180^\circ )).
-
Confusing triangle angle relationships: When calculating angles in triangles, ensure the sum equals ( 180^\circ ).
AI-generated content may contain errors. Please verify critical information