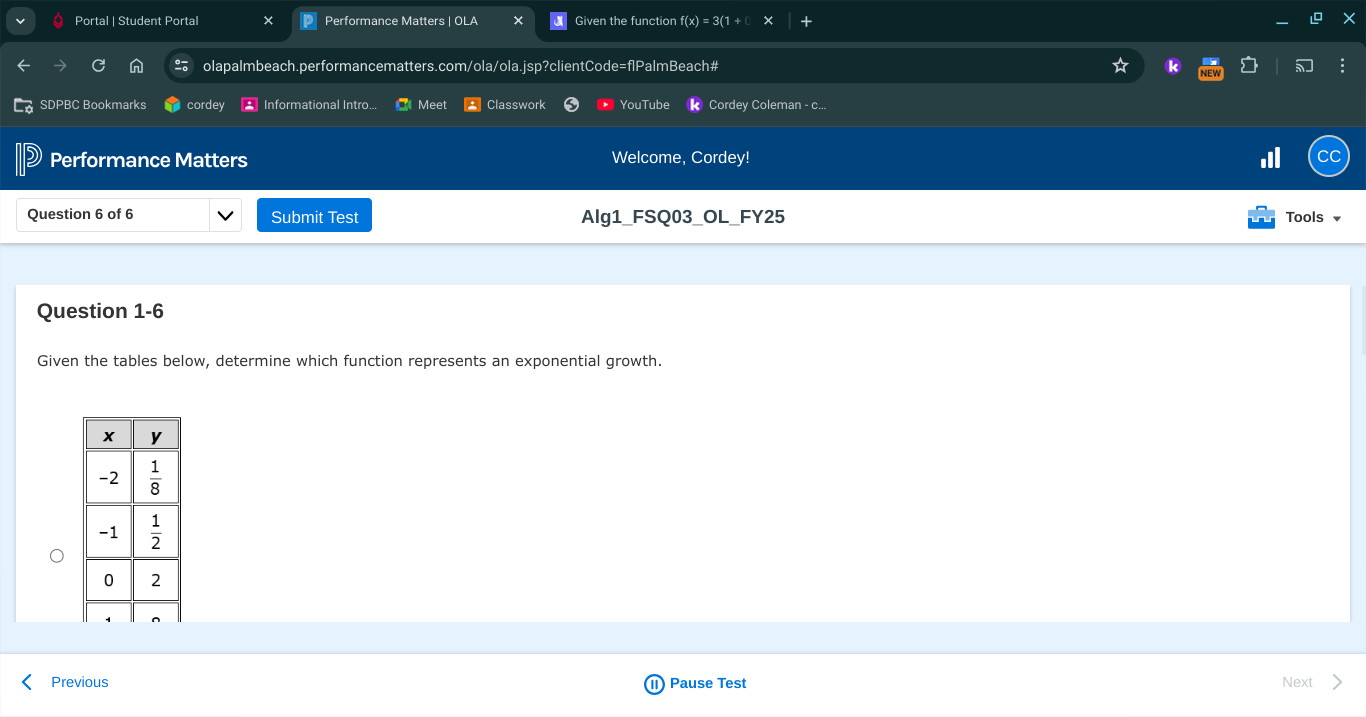
Given the tables below, determine which function represents an exponential growth.
Understand the Problem
The question is asking to analyze the provided tables to determine which function illustrates exponential growth. This involves examining the relationship between the x and y values to identify the nature of their growth pattern.
Answer
The function does not represent exponential growth.
Answer for screen readers
The function does not represent exponential growth due to the inconsistently changing ratios of the $y$ values.
Steps to Solve
-
Identify Exponential Growth Exponential growth occurs when the rate of growth of a quantity is proportional to its current value. In simpler terms, as the x values increase, the y values should grow by a consistent multiplicative factor.
-
Examine the Given Data Look at the pairs of $(x, y)$ values provided in the table:
| $x$ | $y$ |
|---|---|
| -2 | 1/8 |
| -1 | 1/2 |
| 0 | 2 |
| 1 | 6 |
| 2 | 18 |
- Calculate Ratios For each consecutive x value, calculate the ratio of $y$ values to check for a consistent multiplicative factor:
-
From $y(-2) = \frac{1}{8}$ to $y(-1) = \frac{1}{2}$ is:
$$ \text{Ratio} = \frac{1/2}{1/8} = 4 $$ -
From $y(-1) = \frac{1}{2}$ to $y(0) = 2$:
$$ \text{Ratio} = \frac{2}{1/2} = 4 $$ -
From $y(0) = 2$ to $y(1) = 6$:
$$ \text{Ratio} = \frac{6}{2} = 3 $$ -
From $y(1) = 6$ to $y(2) = 18$:
$$ \text{Ratio} = \frac{18}{6} = 3 $$
-
Observing the Growth Pattern Notice the multiplicative factors. The ratios from the first few calculations (4) followed by (3) suggest a changing growth rate.
-
Conclusion about the Growth Nature Since the ratio of y-values changes, this indicates that the relationship does not consistently exhibit exponential growth throughout but may show some characteristics of polynomial or mixed growth.
The function does not represent exponential growth due to the inconsistently changing ratios of the $y$ values.
More Information
Exponential functions typically require a consistent ratio of $y$ values as $x$ changes. In this case, the ratios change, indicating that the growth is not purely exponential.
Tips
- Assuming that if any ratios are the same, the function is exponential without checking all ratios.
- Misinterpreting the values; ensure you are comparing consecutive $y$ values rather than arbitrary selections.
AI-generated content may contain errors. Please verify critical information