1. Déterminer les valeurs de la moyenne et de l'écart type. 2. Trouver les intervalles de confiance de ces paramètres à 90%. 3. Estimer la pluie décenale et son intervalle de confi... 1. Déterminer les valeurs de la moyenne et de l'écart type. 2. Trouver les intervalles de confiance de ces paramètres à 90%. 3. Estimer la pluie décenale et son intervalle de confiance à 80%.
Understand the Problem
La question demande de déterminer des valeurs statistiques à partir d'un échantillon de données de pluie. Les trois sous-questions se concentrent sur le calcul des valeurs centrales, les intervalles de confiance et l'estimation d'une variable avec un intervalle de confiance spécifique.
Answer
La moyenne doit être calculée comme $\bar{x}$, l'écart type comme $s$, et les intervalles de confiance pour la moyenne et la pluie décenale sont donnés par les équations ci-dessus.
Answer for screen readers
- La moyenne des précipitations annuelles $\bar{x}$ et l'écart type $s$ doivent être calculés en utilisant les données fournies.
- L'intervalle de confiance pour ces paramètres à 90% sera donné par :
$$ IC = \bar{x} \pm t \times \frac{s}{\sqrt{25}} $$
- Pour la pluie décenale, l'estimation est :
$$ \text{Pluie décenale} = 10 \cdot \bar{x} $$
Et l'intervalle de confiance à 80% est :
$$ IC_{décennal} = (10 \cdot \bar{x}) \pm t \times \frac{s}{\sqrt{25}} \times 10 $$
Steps to Solve
- Calculer la moyenne ($\bar{x}$)
La moyenne est calculée en additionnant toutes les valeurs des précipitations annuelles et en divisant par le nombre d'années.
$$ \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} $$
où $x_i$ est la valeur des précipitations annuelles et $n$ est le nombre d'années (25 dans ce cas).
- Calculer l'écart type ($s$)
L'écart type mesure la dispersion des valeurs par rapport à la moyenne. Il se calcule comme suit :
$$ s = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n - 1}} $$
où $x_i$ est chaque valeur et $\bar{x}$ est la moyenne calculée précédemment.
- Calculer l'intervalle de confiance à 90%
Pour déterminer l'intervalle de confiance à 90%, utilisez la formule suivante :
$$ IC = \bar{x} \pm t \times \frac{s}{\sqrt{n}} $$
où $t$ est la valeur critique pour un niveau de confiance de 90% et $n$ est le nombre de mesures.
- Estimer la pluie décenale avec son intervalle de confiance à 80%
Pour estimer les précipitations d'une décennie, multipliez simplement la moyenne annuelle par 10. Puis, appliquez la même méthode d'intervalle de confiance pour 80% :
$$ IC_{décennal} = (10 \cdot \bar{x}) \pm t \times \frac{s}{\sqrt{n}} \times 10 $$
- Utilisation de la droite de Henry
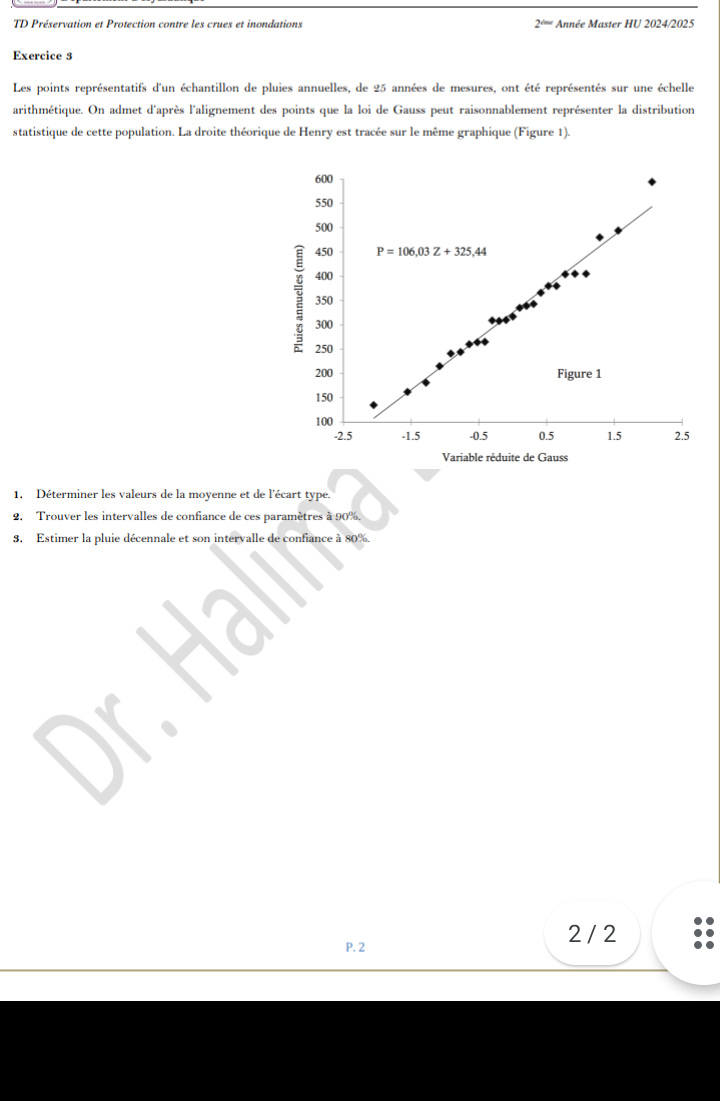
La droite de Henry ($P = 106,03 Z + 325,44$) peut également être utilisée pour estimer les précipitations en fonction des valeurs réduites de Gauss. En utilisant les valeurs de Z pour calculer les précipitations.
- La moyenne des précipitations annuelles $\bar{x}$ et l'écart type $s$ doivent être calculés en utilisant les données fournies.
- L'intervalle de confiance pour ces paramètres à 90% sera donné par :
$$ IC = \bar{x} \pm t \times \frac{s}{\sqrt{25}} $$
- Pour la pluie décenale, l'estimation est :
$$ \text{Pluie décenale} = 10 \cdot \bar{x} $$
Et l'intervalle de confiance à 80% est :
$$ IC_{décennal} = (10 \cdot \bar{x}) \pm t \times \frac{s}{\sqrt{25}} \times 10 $$
More Information
La moyenne et l'écart type sont des statistiques descriptives essentielles pour comprendre la distribution des données. L'intervalle de confiance vous donne une estimation de la précision de la moyenne à partir des données échantillonnées. En multipliant la moyenne par 10, nous pouvons comprendre les tendances décennales des précipitations.
Tips
- Ne pas utiliser le bon facteur de correction pour l'écart type, lorsqu'on passe d'un échantillon à une population, il est important de prendre en compte $n-1$ pour l'estimation de l'écart type.
- Confondre les niveaux de confiance et utiliser le mauvais t-statistique. Il est crucial d'utiliser la bonne table pour trouver la valeur critique correspondante au niveau de confiance souhaité.
AI-generated content may contain errors. Please verify critical information