Given the right triangle below, determine the distance of line segment AB. Round your final answer to the nearest tenth.
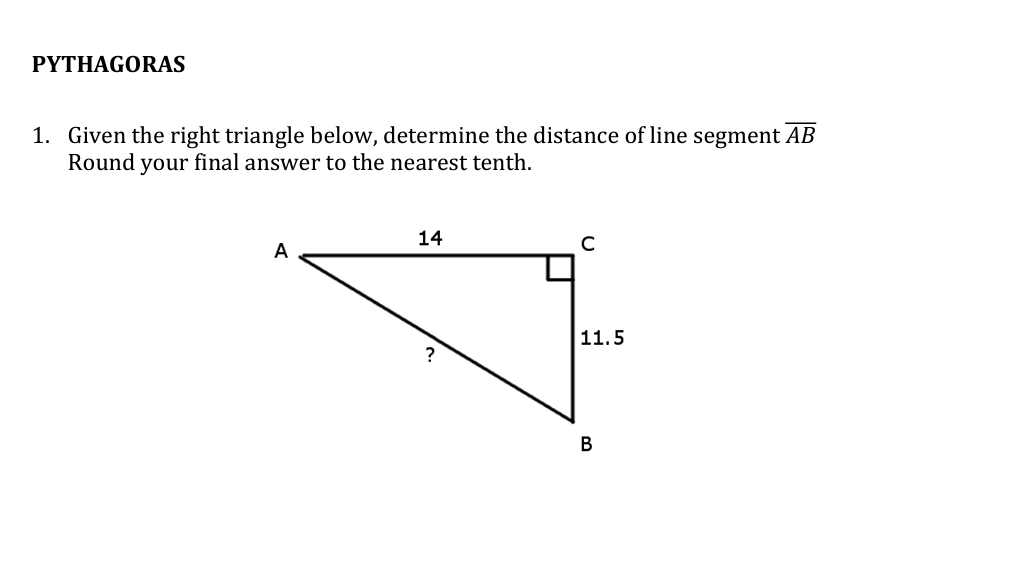
Understand the Problem
The question is asking to determine the length of line segment AB in a right triangle using the Pythagorean theorem. We will identify known lengths and apply the theorem to find the missing side.
Answer
The length of line segment \( \overline{AB} \) is \( 8.0 \).
Answer for screen readers
The length of line segment ( \overline{AB} ) is ( 8.0 ).
Steps to Solve
- Identify the known values in the triangle
In the right triangle ABC, we know the lengths of AC and BC. AC = 14 and BC = 11.5. We will find the length of AB, which we denote as $x$.
- Apply the Pythagorean theorem
The Pythagorean theorem states that in a right triangle, the sum of the squares of the lengths of the two shorter sides equals the square of the length of the hypotenuse. The equation is expressed as:
$$ c^2 = a^2 + b^2 $$
Here, $c$ is the hypotenuse (AC), and $a$ and $b$ are the other two sides (AB and BC).
- Set up the equation using known values
Substituting the known values into the equation gives:
$$ 14^2 = x^2 + 11.5^2 $$
Calculating the squares:
$$ 196 = x^2 + 132.25 $$
- Isolate $x^2$
Rearranging the equation to solve for $x^2$:
$$ x^2 = 196 - 132.25 $$
Calculating the right side:
$$ x^2 = 63.75 $$
- Calculate $x$
To find $x$, take the square root of $x^2$:
$$ x = \sqrt{63.75} $$
Calculating the square root gives:
$$ x \approx 7.99 $$
- Round to the nearest tenth
Finally, rounding $x$ to the nearest tenth:
$$ x \approx 8.0 $$
The length of line segment ( \overline{AB} ) is ( 8.0 ).
More Information
The Pythagorean theorem is fundamental in geometry and is used for calculating the sides of right triangles. This problem illustrates how to apply the theorem in practical situations.
Tips
- Misapplying the theorem: Ensure you always identify which side is the hypotenuse and which are the legs.
- Calculation errors: Be careful when squaring numbers and performing square roots.
AI-generated content may contain errors. Please verify critical information