Given the right triangle below, determine the distance of line segment AB. Round your final answer to the nearest tenth.
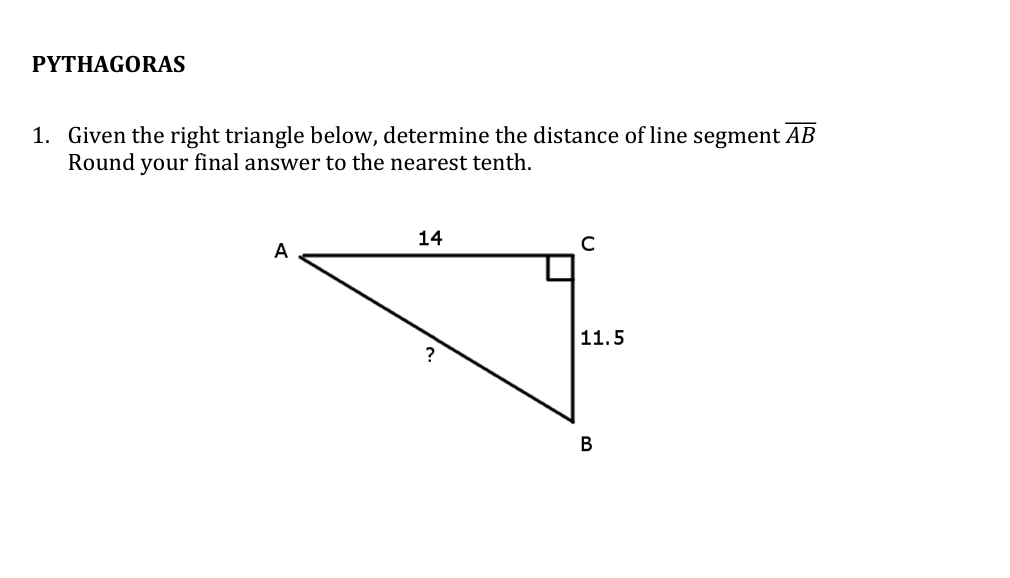
Understand the Problem
The question is asking to determine the length of line segment AB in a right triangle using the Pythagorean theorem. We know two side lengths: AC equals 14 and BC equals 11.5. We will use the theorem, which states that in a right triangle, the square of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC).
Answer
The length of line segment $AB$ is approximately $8.0$.
Answer for screen readers
The length of line segment $AB$ is approximately $8.0$.
Steps to Solve
-
Identify the sides of the triangle In the right triangle, side $AC$ is the hypotenuse with a length of 14, side $BC$ is one leg with a length of 11.5, and side $AB$ is the other leg, which we need to find.
-
Apply the Pythagorean theorem The Pythagorean theorem states that for a right triangle: $$ AC^2 = AB^2 + BC^2 $$ Here, we will substitute the known values into the equation: $$ 14^2 = AB^2 + 11.5^2 $$
-
Calculate the squares of the known lengths Now we calculate the squares: $$ 14^2 = 196 $$ $$ 11.5^2 = 132.25 $$
-
Set up the equation to find $AB^2$ Substituting into the equation gives: $$ 196 = AB^2 + 132.25 $$
-
Subtract $132.25$ from both sides To isolate $AB^2$, subtract 132.25 from both sides: $$ AB^2 = 196 - 132.25 $$ $$ AB^2 = 63.75 $$
-
Take the square root of both sides Now, to find $AB$, take the square root: $$ AB = \sqrt{63.75} \approx 7.993 $$
-
Round to the nearest tenth Finally, we round to the nearest tenth: $$ AB \approx 8.0 $$
The length of line segment $AB$ is approximately $8.0$.
More Information
The Pythagorean theorem is a powerful tool in geometry that applies to right triangles, allowing us to relate the lengths of the sides. By solving for unknown sides, we can find distances in various contexts.
Tips
- Forgetting to square the lengths when applying the Pythagorean theorem.
- Not rounding the final answer to the correct decimal place as specified in the problem.
- Mixing up which side is the hypotenuse versus which are the legs of the triangle.
AI-generated content may contain errors. Please verify critical information