What is the equation of the circle represented in the image?

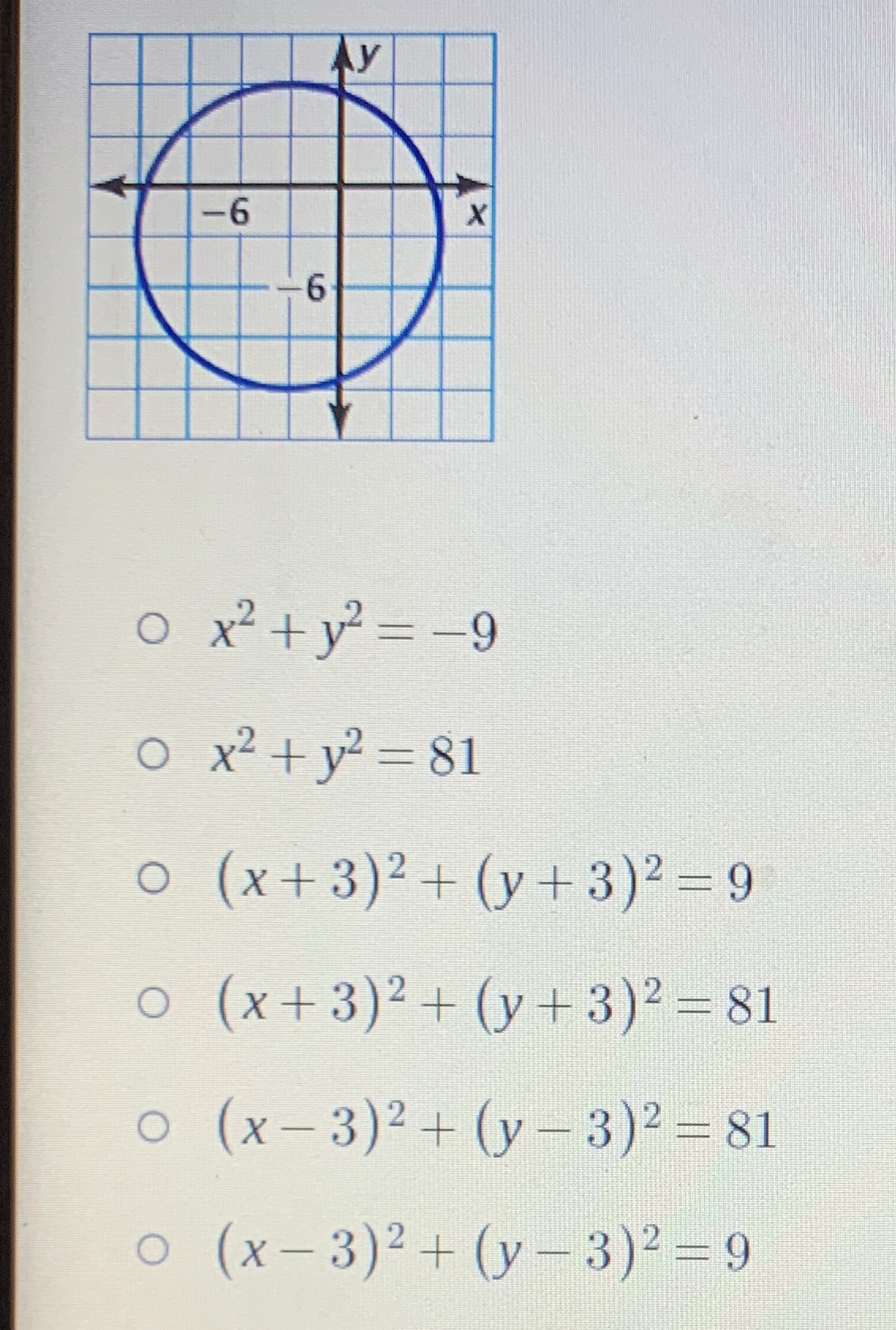
Understand the Problem

The question is asking for the correct equation of the circle depicted in the image, which has a specific center and radius. The high-level approach involves identifying the characteristics of the circle based on the grid and selecting the correct algebraic representation from the provided options.

Answer

The equation of the circle is $$(x + 3)^2 + (y + 3)^2 = 9$$.

Steps to Solve

Identify the Center and Radius of the Circle

From the image, determine the coordinates of the circle's center and its radius. The center appears to be located at $(-3, -3)$, and the radius is $3$ units since it goes from $-3$ to $0$ on both axes.

Write the Standard Equation of a Circle

The standard equation of a circle with center $(h, k)$ and radius $r$ is given by the formula:

$$(x - h)^2 + (y - k)^2 = r^2$$

Here, $h = -3$ and $k = -3$, and the radius $r = 3$, so:

$$(x + 3)^2 + (y + 3)^2 = 3^2$$

Calculate the Square of the Radius

Calculating $r^2$ gives:

$$3^2 = 9$$

Substitute Back into the Equation of the Circle

Substituting the values into the standard equation yields:

$$(x + 3)^2 + (y + 3)^2 = 9$$

Identify the Correct Option

Now, compare this derived equation with the options provided to select the correct one.

The correct equation of the circle is $$(x + 3)^2 + (y + 3)^2 = 9$$.

More Information

This equation represents a circle centered at $(-3, -3)$ with a radius of $3$. The square of the radius, $9$, determines the size of the circle.

Tips

Misidentifying the center of the circle: It's crucial to carefully observe the graph to get the center coordinates correct.
Confusing the radius with the diameter: Remember, the radius is half of the diameter.
Failing to square the radius when writing the equation: Ensure $r^2$ is correctly calculated as it impacts the equation.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!