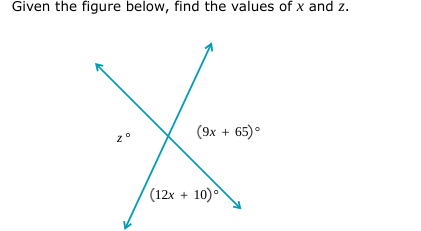
Given the figure below, find the values of x and z.
Understand the Problem
The question is asking to find the values of x and z given the relationships between angles formed by intersecting lines. We will set up equations based on the fact that vertically opposite angles are equal and solve for the unknowns.
Answer
$x = \frac{55}{3}, z = 230$
Answer for screen readers
The values are:
$x = \frac{55}{3}$ or approximately $18.33$,
$z = 230$.
Steps to Solve
-
Identify Vertically Opposite Angles
The angles formed by the intersecting lines are vertically opposite angles. Therefore, we can equate the angles: $$ (9x + 65) = (12x + 10) $$ -
Set Up the Equation
Start by rearranging the equation to isolate the variable $x$: $$ 9x + 65 = 12x + 10 $$ -
Rearrange to Solve for x
Subtract $9x$ from both sides: $$ 65 = 12x - 9x + 10 $$
This simplifies to: $$ 65 = 3x + 10 $$ -
Isolate x
Now, subtract 10 from both sides: $$ 65 - 10 = 3x $$
This simplifies to: $$ 55 = 3x $$ -
Divide by 3
To find $x$, divide both sides by 3: $$ x = \frac{55}{3} $$
This yields: $$ x \approx 18.33 $$ -
Find z
Now that we have $x$, substitute it back into either angle expression to find $z$. We'll use the equation for $z$: $$ z = 12x + 10 $$
Substituting for $x$ gives: $$ z = 12\left(\frac{55}{3}\right) + 10 $$ -
Calculate z
Now compute $z$: $$ z = \frac{660}{3} + 10 = 220 + 10 = 230 $$
The values are:
$x = \frac{55}{3}$ or approximately $18.33$,
$z = 230$.
More Information
In the given problem, we utilized properties of vertically opposite angles to set up linear equations that allowed us to solve for the unknown variables. Understanding these angle properties is crucial in geometry, especially when dealing with intersecting lines.
Tips
- Neglecting Vertical Angles: Forgetting that vertically opposite angles are equal can lead to incorrect equations.
- Miscalculating Steps: Be careful with basic arithmetic, especially when combining like terms or distributing terms.
AI-generated content may contain errors. Please verify critical information