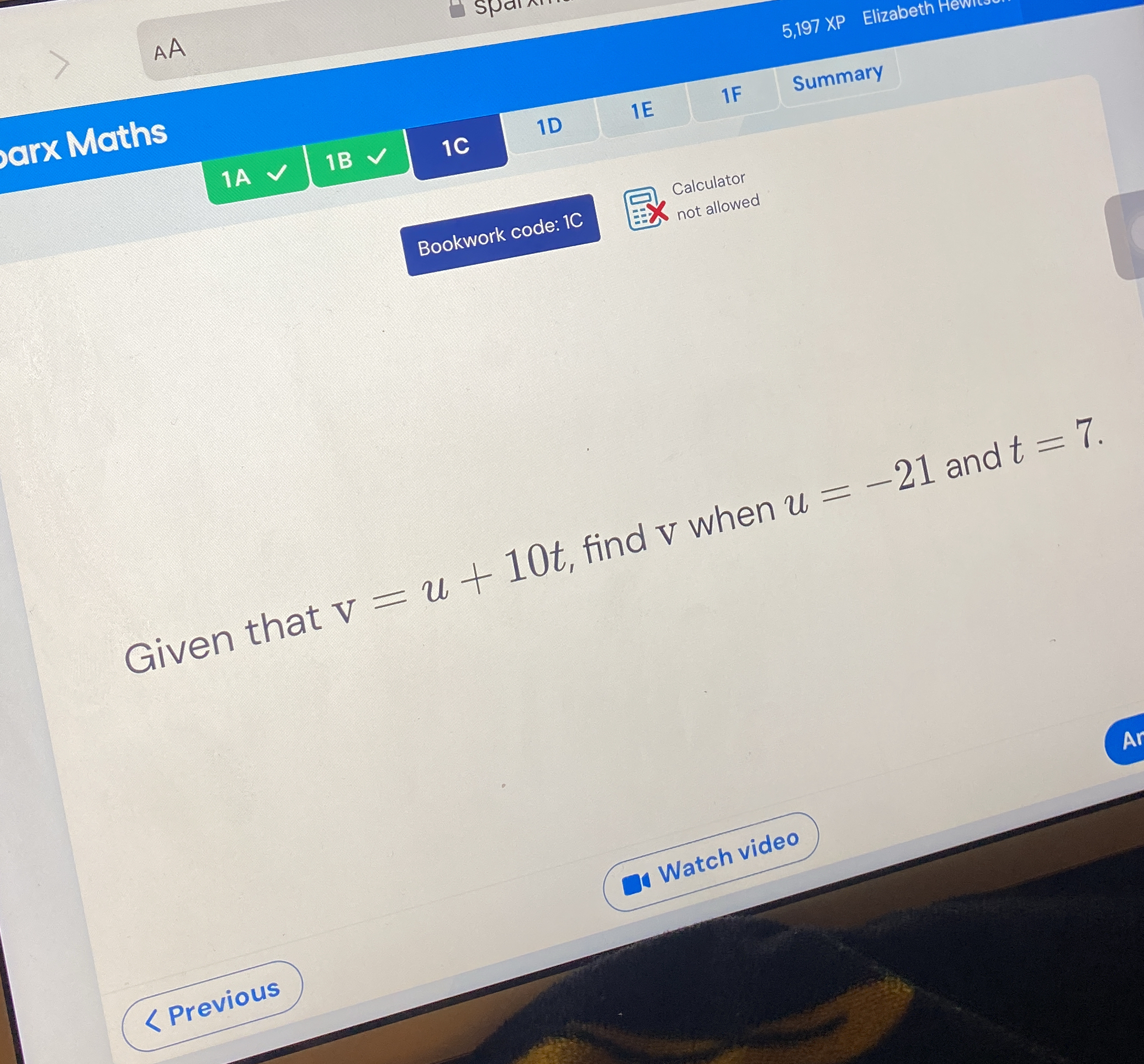
Given that v = u + 10t, find v when u = -21 and t = 7.
Understand the Problem
The question is asking us to find the value of v using the equation v = u + 10t, given specific values for u and t. This is a straightforward substitution problem in algebra.
Answer
$v = 49$
Answer for screen readers
The value of $v$ is $49$.
Steps to Solve
- Identify the given values
We are given the equation $v = u + 10t$ and the values $u = -21$ and $t = 7$.
- Substitute the values into the equation
Now, we substitute the values of $u$ and $t$ into the equation:
$$ v = -21 + 10(7) $$
- Calculate the value of $10t$
Next, we calculate $10t$:
$$ 10(7) = 70 $$
- Complete the substitution
Now substitute $70$ back into the equation:
$$ v = -21 + 70 $$
- Calculate $v$
Finally, we perform the addition:
$$ v = 49 $$
The value of $v$ is $49$.
More Information
The formula $v = u + 10t$ is often used in physics to determine the final velocity when initial conditions and time are known. In this case, a negative initial velocity combined with a positive contribution from the acceleration factor results in a positive final velocity.
Tips
- Not applying the correct signs: Make sure to carefully manage positive and negative values during calculations.
- Forgetting to multiply the time $t$ by $10$: It’s crucial to apply the multiplication before proceeding with the addition.
AI-generated content may contain errors. Please verify critical information