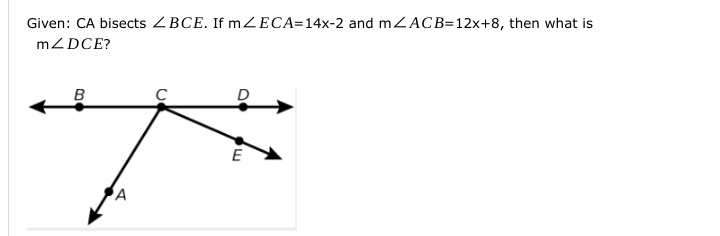
Given that CA bisects angle BCE. If m∠ECA=14x-2 and m∠ACB=12x+8, then what is m∠DCE?
Understand the Problem
The question involves finding the measure of angle DCE given that CA bisects angle BCE. We need to use the properties of angle bisectors and the given expressions for the angles to set up an equation to solve for x and subsequently find the value of m∠DCE.
Answer
The measure of angle \( m∠DCE \) is \( 68 \) degrees.
Answer for screen readers
The measure of angle ( m∠DCE ) is ( 68 ) degrees.
Steps to Solve
- Identify given angles and relationships
Since CA bisects angle BCE, we know that:
$$ m∠ECA = m∠ACB $$
- Set up the equation
Using the expressions provided for the angles:
$$ 14x - 2 = 12x + 8 $$
- Solve for x
First, rearranging the equation gives:
$$ 14x - 12x = 8 + 2 $$
This simplifies to:
$$ 2x = 10 $$
Now, divide both sides by 2:
$$ x = 5 $$
- Substitute x back into one of the angle expressions
To find either angle, substitute $x$ into one of the expressions. Using $m∠ECA$:
$$ m∠ECA = 14(5) - 2 $$
- Calculate m∠ECA
This gives:
$$ m∠ECA = 70 - 2 = 68 \text{ degrees} $$
Since CA bisects angle BCE, we have:
$$ m∠DCE = m∠ECA = 68 \text{ degrees} $$
The measure of angle ( m∠DCE ) is ( 68 ) degrees.
More Information
Angle bisectors split an angle into two equal halves. In this case, because CA bisects ∠BCE, both angles formed, m∠ECA and m∠ACB, are equal to each other at 68 degrees.
Tips
- A common mistake is to forget that the angles are equal due to the angle bisector. Make sure to set both expressions equal to each other.
- Another mistake is miscalculating the arithmetic when solving for ( x ). Always double-check your algebraic manipulations.
AI-generated content may contain errors. Please verify critical information