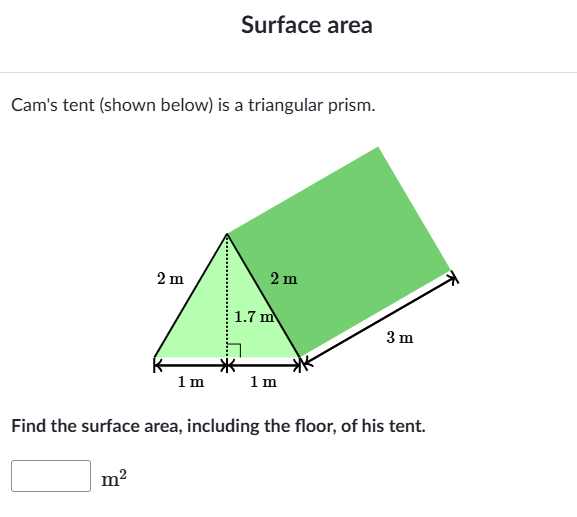
Find the surface area, including the floor, of his tent.

Steps to Solve

1. Identify the Components of the Prism

The triangular prism has two triangular bases and three rectangular sides. We will calculate the areas of these components: the triangular faces and the rectangular sides.

2. Calculate the Area of the Triangular Base

The triangle has a base of $1 , \text{m}$ and a height of $1.7 , \text{m}$. The area ( A ) of a triangle can be calculated using the formula:

$$ A = \frac{1}{2} \times \text{base} \times \text{height} $$

Substituting the values:

$$ A = \frac{1}{2} \times 1 \times 1.7 = 0.85 , \text{m}^2 $$

3. Find the Area of Both Triangular Bases

Since there are two triangular bases, the total area for the triangular bases is:

$$ \text{Total Area of Triangles} = 2 \times 0.85 = 1.7 , \text{m}^2 $$

4. Calculate the Areas of the Rectangular Sides

The rectangular sides have the following dimensions:

• One side with dimensions $1 , \text{m} \times 3 , \text{m}$.
• Two sides with dimensions $2 , \text{m} \times 3 , \text{m}$.

Calculating each area:

• Area of the first rectangle:

$$ A_1 = 1 \times 3 = 3 , \text{m}^2 $$

• Area of the two other rectangles (both are the same):

$$ A_2 = 2 \times 3 = 6 , \text{m}^2 \quad \text{(for one)} $$

Total for both:

$$ \text{Total Area for Rectangles} = 2 \times 6 = 12 , \text{m}^2 $$

5. Calculate the Total Surface Area

The total surface area ( S ) of the prism is calculated by adding the areas of the triangular bases and the rectangular sides:

$$ S = \text{Total Area of Triangles} + \text{Total Area for Rectangles} $$

Substituting the values:

$$ S = 1.7 + 12 = 13.7 , \text{m}^2 $$