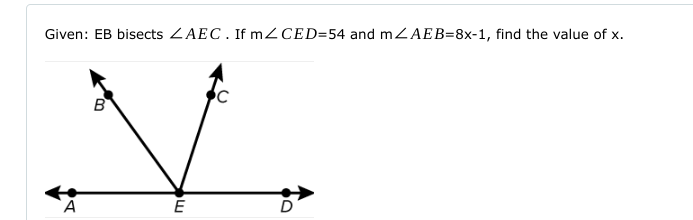
Given: EB bisects ∠AEC. If m∠CED=54 and m∠AEB=8x-1, find the value of x.
Understand the Problem
The question is asking to find the value of x in a geometric situation involving angle bisectors. Given the measures of angles, we can set up an equation to solve for x.
Answer
$x = \frac{55}{8}$ or $6.875$
Answer for screen readers
The value of $x$ is $6.875$ or $\frac{55}{8}$.
Steps to Solve
-
Identify the angles From the problem, we know that $EB$ bisects $\angle AEC$. Therefore, we can express $\angle AEB$ in terms of the angles provided: $$ m\angle AEC = m\angle AEB + m\angle CED $$
-
Set up the equation Given that $m\angle CED = 54^\circ$ and $m\angle AEB = 8x - 1$, we can substitute these values into the angle bisector equation: $$ m\angle AEC = m\angle AEB + m\angle CED $$
-
Express angle AEC Since $EB$ bisects $\angle AEC$: $$ m\angle AEC = 2 \cdot m\angle AEB $$ Thus: $$ m\angle AEC = 2(8x - 1) $$
-
Combine the equations Now set the two expressions for $m\angle AEC$ equal to each other: $$ 2(8x - 1) = (8x - 1) + 54 $$
-
Simplify and solve for x Expand and simplify: $$ 16x - 2 = 8x + 53 $$ Now subtract $8x$ from both sides: $$ 8x - 2 = 53 $$
-
Isolate x Add 2 to both sides: $$ 8x = 55 $$ Now, divide both sides by 8: $$ x = \frac{55}{8} $$
The value of $x$ is $6.875$ or $\frac{55}{8}$.
More Information
The angle bisector theorem is applied here, allowing us to equate the angles and solve for $x$. The final answer indicates that the ratio of the angles is maintained.
Tips
- Misunderstanding the angle relationships can lead to incorrect equations. Always confirm whether the angle is bisected or related in another way.
- Forgetting to multiply the angle expression when dealing with bisected angles can lead to incorrect values.
AI-generated content may contain errors. Please verify critical information