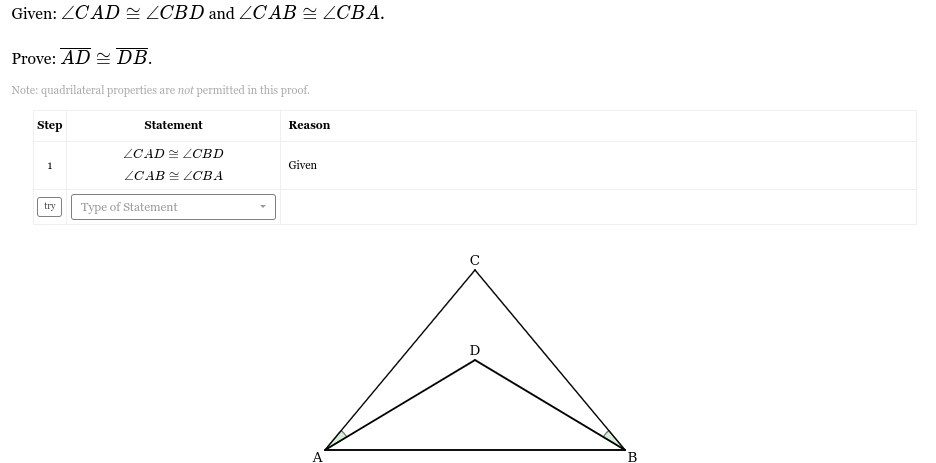
Given: ∠CAD ≅ ∠CBD and ∠CAB ≅ ∠CBA. Prove: AD ≅ DB.
Understand the Problem
The question is asking to prove that segments AD and DB are congruent based on the given angle congruences. The approach involves logical steps of geometric proof using the provided information.
Answer
$AD \cong DB$
Answer for screen readers
$AD \cong DB$
Steps to Solve
- List Known Angle Congruences
From the problem, we know: $$ \angle CAD \cong \angle CBD \quad \text{(given)} $$ $$ \angle CAB \cong \angle CBA \quad \text{(given)} $$
- Identify Triangles for Analysis
We can focus on triangles $ACD$ and $BCD$. We have two pairs of congruent angles:
- $\angle CAD \cong \angle CBD$
- $\angle CAB \cong \angle CBA$
- Apply the Angle-Angle Criterion for Triangle Congruence
Since we have two pairs of congruent angles in triangles $ACD$ and $BCD$, we can say: $$ \triangle ACD \cong \triangle BCD \quad \text{(by AA criterion)} $$
- Conclude with the Corresponding Segments
From the congruence of the triangles, we can state that corresponding sides are congruent: $$ AD \cong DB \quad \text{(corresponding sides of congruent triangles)} $$
$AD \cong DB$
More Information
The proof establishes that angle congruences lead to triangle congruences. In this case, using the Angle-Angle (AA) criterion is sufficient to conclude that the non-included sides (segments) are equal in length.
Tips
- Neglecting to include all necessary angles: Make sure all relevant angles are accounted for when applying angle congruences.
- Assuming triangles are congruent without justification: Always use the criteria explicitly (like AA) rather than only stating angles are equal.
AI-generated content may contain errors. Please verify critical information