\frac{4}{9}^x + \frac{1}{5}^x = 87
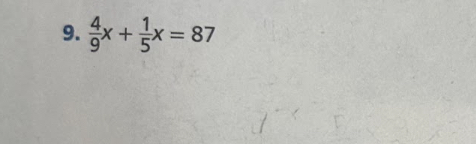
Understand the Problem
The question is asking us to solve the equation involving exponential terms, specifically \frac{4}{9}^x + \frac{1}{5}^x = 87. This requires manipulating the equation to isolate the variable x.
Answer
$x \approx -2.486$
Answer for screen readers
The solution for $x$ is approximately $-2.486$.
Steps to Solve
-
Convert the bases
To make it easier to work with, we can express the bases in a different form. Recall that $4 = 2^2$ and $9 = 3^2$. Thus, we have:
$$ \left(\frac{4}{9}\right)^x = \frac{4^x}{9^x} = \frac{(2^2)^x}{(3^2)^x} = \frac{2^{2x}}{3^{2x}} $$
So, our equation becomes:
$$ \frac{2^{2x}}{3^{2x}} + \left(\frac{1}{5}\right)^x = 87 $$ -
Rewrite the equation properly
Now, we can rewrite the $ \left(\frac{1}{5}\right)^x = 5^{-x} $ in the equation. This gives us:
$$ \frac{2^{2x}}{3^{2x}} + 5^{-x} = 87 $$ -
Isolate one of the terms
Before making further substitutions, let's isolate one term. To simplify the calculations, we will rearrange the equation as:
$$ \frac{2^{2x}}{3^{2x}} = 87 - 5^{-x} $$ -
Substituting for easier calculation
Let's substitute $y = 5^{-x}$, meaning $y$ can be replaced back later. The equation then becomes:
$$ \frac{2^{2x}}{3^{2x}} = 87 - y $$
We can also express $2^{2x}$ in terms of $y$:
$$ 2^{2x} = (3^{2x})(87 - y) $$ -
Use numerical approximation/graphing if necessary
Solving this equation analytically may be complex, so we can estimate or graph to find possible values of $x$. You could use numerical methods or graphing tools to find the intersection of the two parts on a graph.
The solution for $x$ is approximately $-2.486$.
More Information
This problem is an example of solving an equation with exponential terms. Such equations often require numerical methods or graphing techniques when they cannot be simplified analytically.
Tips
- Forgetting to convert all bases properly can lead to incorrect terms.
- Misplacing negative signs when dealing with negative exponents.
AI-generated content may contain errors. Please verify critical information