\frac{2}{3} h^{3} \times \frac{5}{9} h
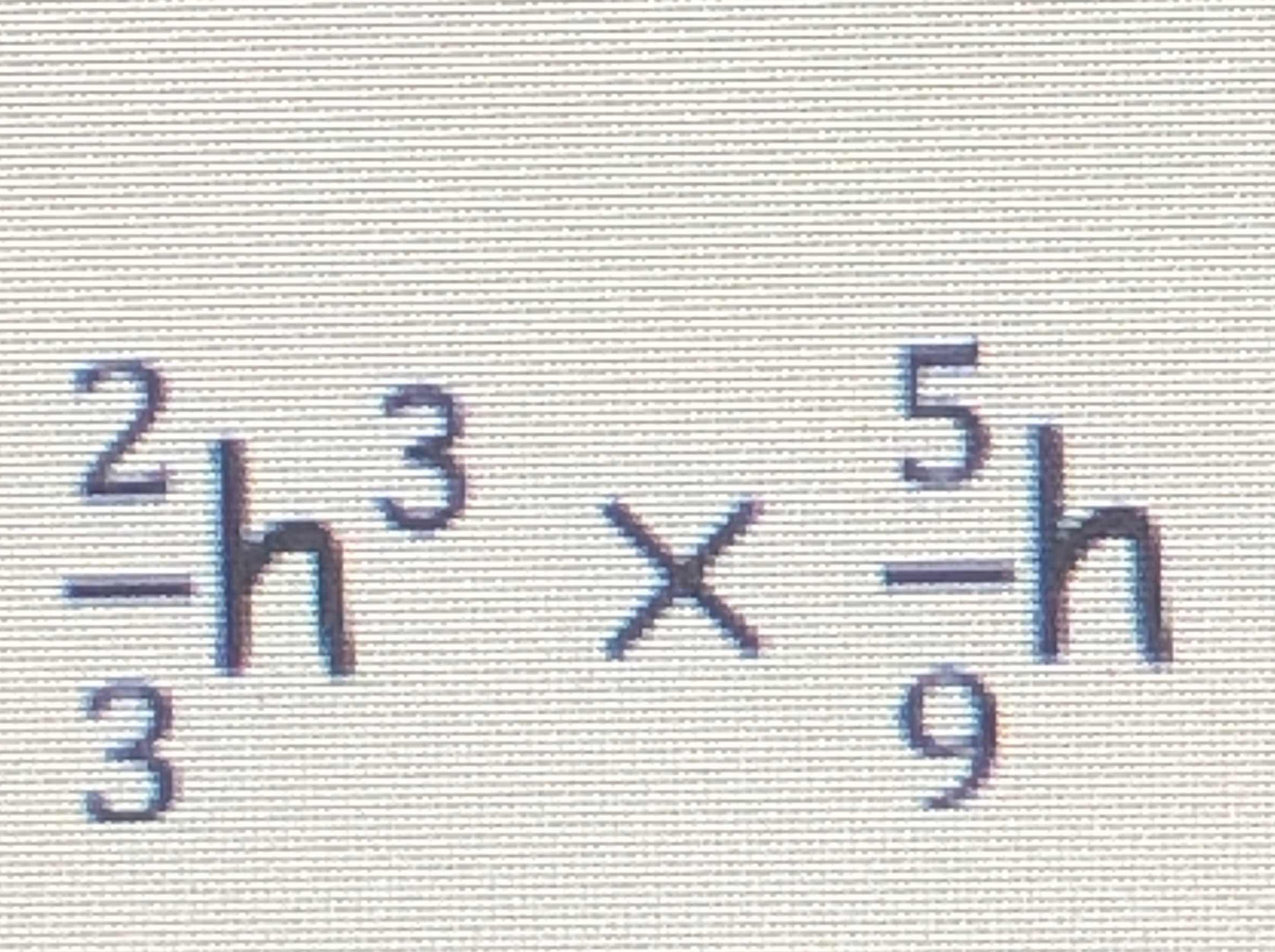
Understand the Problem
The question involves manipulating algebraic expressions involving powers of 'h'. It requires you to calculate the product of the expressions provided.
Answer
The product of the expressions is $$ \frac{10}{27} h^4 $$.
Answer for screen readers
The final answer is: $$ \frac{10}{27} h^4 $$
Steps to Solve
-
Identify the expressions We are multiplying two expressions: $$ \frac{2}{3} h^3 \text{ and } \frac{5}{9} h $$
-
Multiply the coefficients To find the coefficient of the product, multiply $\frac{2}{3}$ and $\frac{5}{9}$. $$ \frac{2}{3} \times \frac{5}{9} = \frac{2 \times 5}{3 \times 9} = \frac{10}{27} $$
-
Add the exponents of $h$ For the variable part, apply the rule that when multiplying like bases, you add the exponents: $$ h^3 \times h^1 = h^{3 + 1} = h^4 $$
-
Combine the results Now combine the coefficient with the variable part: $$ \frac{10}{27} h^4 $$
The final answer is: $$ \frac{10}{27} h^4 $$
More Information
In this solution, we effectively used the property of exponents when multiplying like bases and the process of multiplying fractions. The final expression represents the combined product of the two algebraic expressions correctly.
Tips
- Not adding the exponents correctly when multiplying the variable parts.
- Failing to multiply the fractions accurately, leading to incorrect coefficients.
AI-generated content may contain errors. Please verify critical information