For what choices of α, β and γ does the function have a second order derivatives at x = 1?
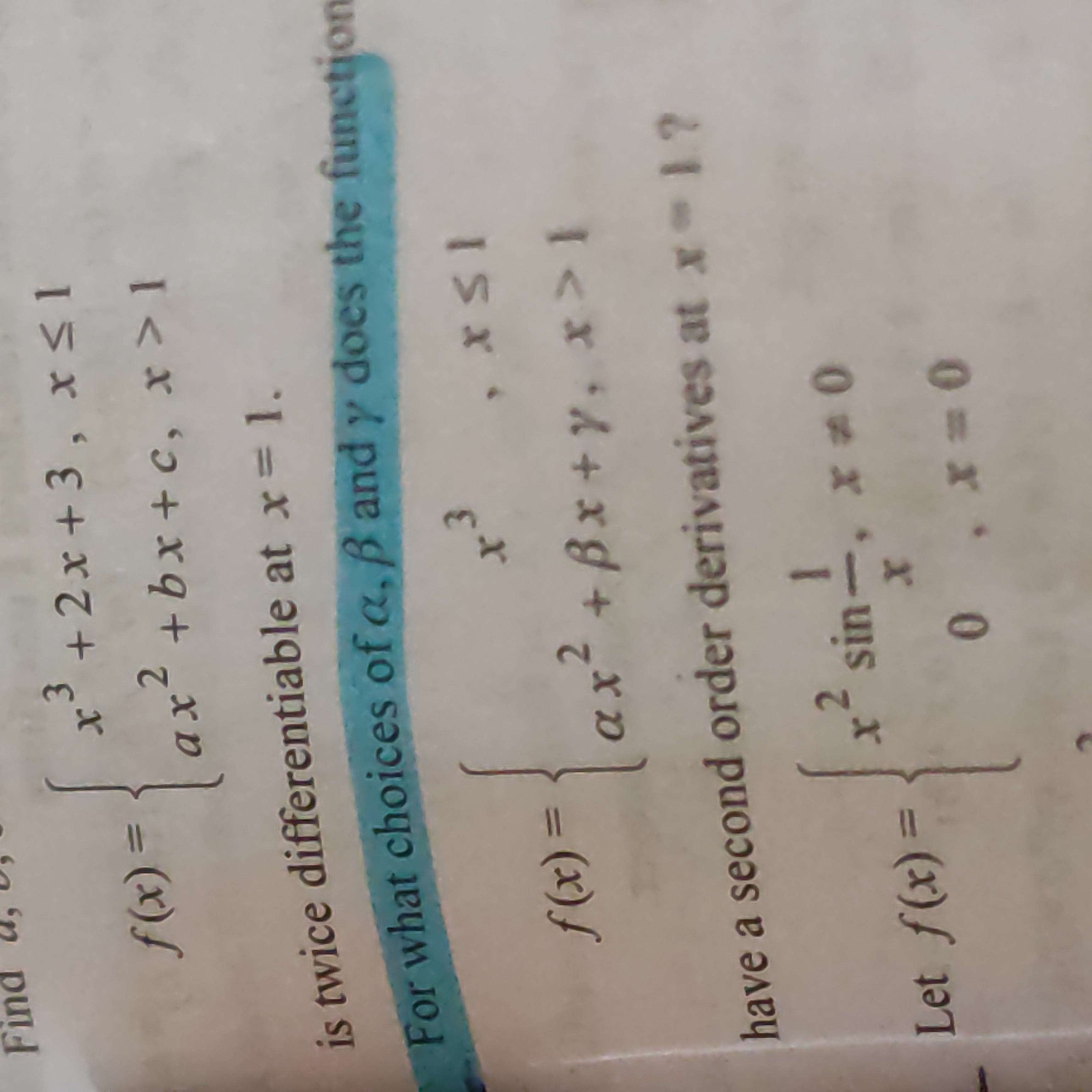
Understand the Problem
The question is asking for the specific values of the parameters α, β, and γ that ensure the given piecewise function is twice differentiable at x = 1. This involves checking conditions for continuity and the existence of first and second derivatives at that point.
Answer
$\alpha = 3$, $\beta = -1$, $\gamma = 4$.
Answer for screen readers
The values are $\alpha = 3$, $\beta = -1$, and $\gamma = 4$.
Steps to Solve
- Continuity at $x = 1$
To ensure the function is continuous at $x = 1$, the two pieces must be equal at that point: $$ \alpha(1)^2 + \beta(1) + \gamma = 1^3 + 2(1) + 3 $$ This simplifies to: $$ \alpha + \beta + \gamma = 6 $$
- First Derivative Continuity at $x = 1$
Next, we need the first derivatives of both pieces to be equal at $x = 1$. The derivative of the first piece is: $$ f'(x) = 3x^2 + 2 $$ Evaluating at $x = 1$ gives: $$ f'(1) = 3(1)^2 + 2 = 5 $$
For the second piece, the derivative is: $$ f'(x) = 2\alpha x + \beta $$ Evaluating at $x = 1$ gives: $$ 2\alpha + \beta = 5 $$
- Second Derivative Continuity at $x = 1$
Finally, the second derivatives must be equal at $x = 1$. The second derivative of the first piece is: $$ f''(x) = 6x $$ Evaluating at $x = 1$ gives: $$ f''(1) = 6(1) = 6 $$
For the second piece, the second derivative is: $$ f''(x) = 2\alpha $$ Setting them equal gives: $$ 2\alpha = 6 \implies \alpha = 3 $$
- Substituting for $\alpha$
Substituting $\alpha = 3$ into the equations:
- From continuity: $$ 3 + \beta + \gamma = 6 \implies \beta + \gamma = 3 $$
- From first derivative continuity: $$ 2(3) + \beta = 5 \implies 6 + \beta = 5 \implies \beta = -1 $$
- Finding $\gamma$
Substituting $\beta = -1$ into $\beta + \gamma = 3$ gives: $$ -1 + \gamma = 3 \implies \gamma = 4 $$
The values are $\alpha = 3$, $\beta = -1$, and $\gamma = 4$.
More Information
These values ensure that the function is not only continuous at $x = 1$, but also has matching first and second derivatives, confirming that it is twice differentiable.
Tips
- Failing to apply the conditions for both continuity and derivative equalities.
- Mixing up the evaluation points between original function and derivatives.
AI-generated content may contain errors. Please verify critical information