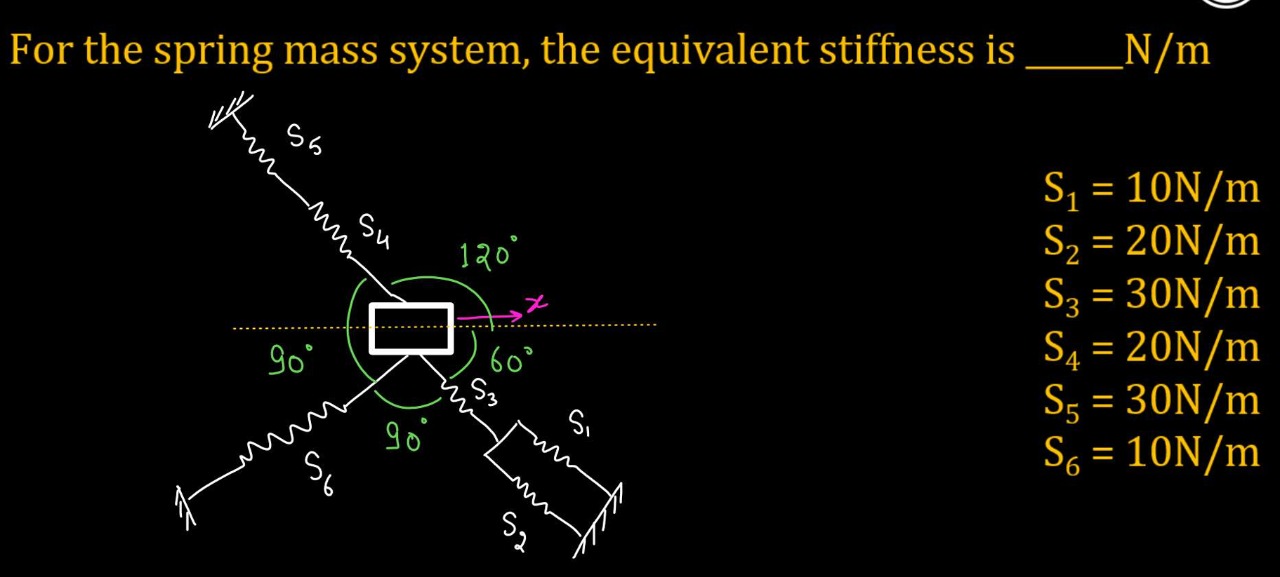
For the spring mass system, the equivalent stiffness is _____ N/m.

Steps to Solve

1. Identify the Spring Arrangements The springs $S_1$ to $S_3$ are arranged at angles of $90^\circ$, $60^\circ$, and $120^\circ$ respectively, while $S_4$ to $S_6$ also make similar angles around a central point.

2. Calculate the Components of Each Spring Stiffness When springs are arranged at an angle, we need to resolve their stiffness into horizontal and vertical components. The horizontal ($k_x$) and vertical ($k_y$) components can be calculated using:

• For $S_1$ and $S_6$:

  • $k_{1x} = S_1 \cdot \cos(90^\circ) = S_1 \cdot 0 = 0$
  • $k_{6x} = S_6 \cdot \cos(90^\circ) = S_6 \cdot 0 = 0$

• For $S_2$:

  • $k_{2x} = S_2 \cdot \cos(0^\circ) = 20 \cdot 1 = 20$

• For $S_3$:

  • $k_{3x} = S_3 \cdot \cos(60^\circ) = 30 \cdot 0.5 = 15$

• For $S_4$:

  • $k_{4x} = S_4 \cdot \cos(120^\circ) = 20 \cdot (-0.5) = -10$

• For $S_5$:

  • $k_{5x} = S_5 \cdot \cos(0^\circ) = 30 \cdot 1 = 30$

3. Sum the Horizontal Components The total horizontal component stiffness ($k_{eq.x}$) is: $$ k_{eq.x} = k_{1x} + k_{2x} + k_{3x} + k_{4x} + k_{5x} + k_{6x} = 0 + 20 + 15 - 10 + 30 + 0 = 55 \text{ N/m} $$

4. Calculate the Vertical Components Using a similar approach, we can calculate the vertical components:

• For $S_1$:

  • $k_{1y} = S_1 \cdot \sin(90^\circ) = 10 \cdot 1 = 10$

• For $S_2$:

  • $k_{2y} = S_2 \cdot \sin(0^\circ) = 20 \cdot 0 = 0$

• For $S_3$:

  • $k_{3y} = S_3 \cdot \sin(60^\circ) = 30 \cdot \sqrt{3}/2 = 25.98$

• For $S_4$:

  • $k_{4y} = S_4 \cdot \sin(120^\circ) = 20 \cdot \sqrt{3}/2 = 17.32$

• For $S_5$:

  • $k_{5y} = S_5 \cdot \sin(0^\circ) = 30 \cdot 0 = 0$

• For $S_6$:

  • $k_{6y} = S_6 \cdot \sin(90^\circ) = 10 \cdot 1 = 10$

5. Sum the Vertical Components The total vertical component stiffness ($k_{eq.y}$) is: $$ k_{eq.y} = k_{1y} + k_{2y} + k_{3y} + k_{4y} + k_{5y} + k_{6y} = 10 + 0 + 25.98 + 17.32 + 0 + 10 = 63.3 \text{ N/m} $$

6. Calculate the Equivalent Stiffness Using Pythagorean Theorem Using the total horizontal ($k_{eq.x}$) and vertical stiffness ($k_{eq.y}$), the equivalent stiffness ($k_{eq}$) is calculated using the Pythagorean theorem: $$ k_{eq} = \sqrt{(k_{eq.x})^2 + (k_{eq.y})^2} = \sqrt{(55)^2 + (63.3)^2} \approx \sqrt{3025 + 4009.69} \approx \sqrt{7034.69} \approx 83.8 \text{ N/m} $$