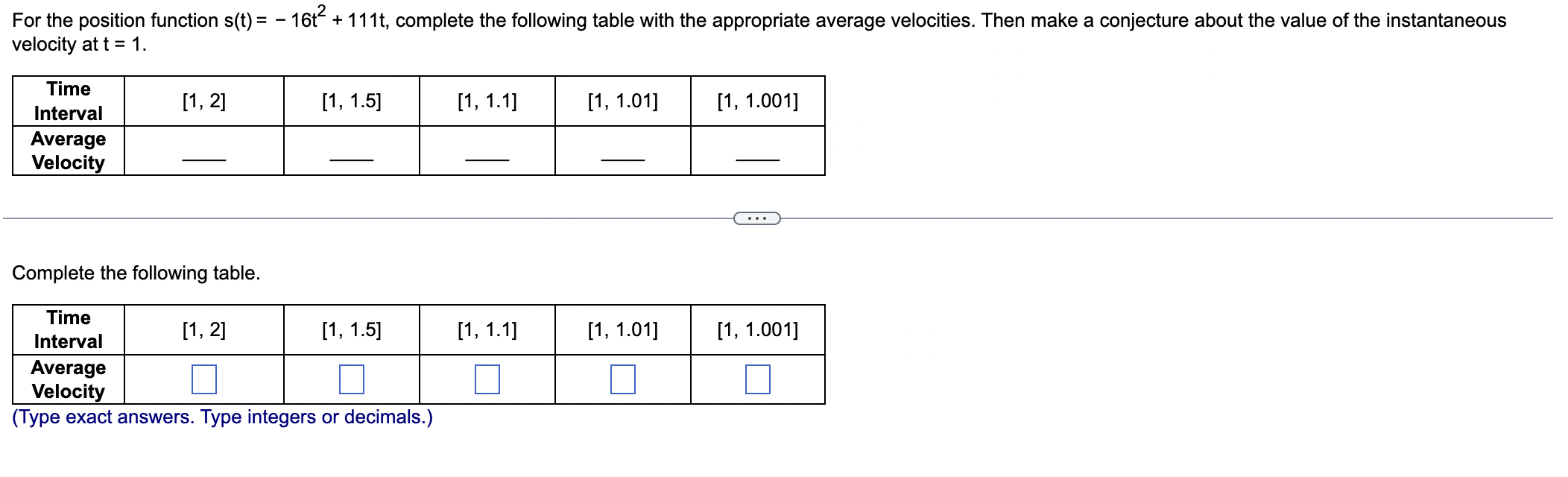
For the position function s(t) = -16t^2 + 111t, complete the table with the appropriate average velocities for the time intervals [1, 2], [1, 1.5], [1, 1.1], [1, 1.01], and [1, 1.1... For the position function s(t) = -16t^2 + 111t, complete the table with the appropriate average velocities for the time intervals [1, 2], [1, 1.5], [1, 1.1], [1, 1.01], and [1, 1.1]. Then make a conjecture about the instantaneous velocity at t = 1. Read more

Steps to Solve

1. Identify the Position Function The position function is given by ( s(t) = -16t^2 + 111t ).

2. Calculate Average Velocity The average velocity over an interval ([a, b]) is given by the formula: $$ V_{avg} = \frac{s(b) - s(a)}{b - a} $$

3. Find Average Velocity for Time Interval ([1, 2])

   • Calculate ( s(2) ) and ( s(1) ):
     • ( s(2) = -16(2)^2 + 111(2) = -64 + 222 = 158 )
     • ( s(1) = -16(1)^2 + 111(1) = -16 + 111 = 95 )
   • Use the average velocity formula: $$ V_{avg}[1, 2] = \frac{158 - 95}{2 - 1} = \frac{63}{1} = 63 $$

4. Find Average Velocity for Time Interval ([1, 1.5])

   • Calculate ( s(1.5) ):
     • ( s(1.5) = -16(1.5)^2 + 111(1.5) = -16(2.25) + 166.5 = -36 + 166.5 = 130.5 )
   • Use the average velocity formula: $$ V_{avg}[1, 1.5] = \frac{130.5 - 95}{1.5 - 1} = \frac{35.5}{0.5} = 71 $$

5. Find Average Velocity for Time Interval ([1, 1.1])

   • Calculate ( s(1.1) ):
     • ( s(1.1) = -16(1.1)^2 + 111(1.1) = -16(1.21) + 122.1 = -19.36 + 122.1 = 102.74 )
   • Use the average velocity formula: $$ V_{avg}[1, 1.1] = \frac{102.74 - 95}{1.1 - 1} = \frac{7.74}{0.1} = 77.4 $$

6. Find Average Velocity for Time Interval ([1, 1.01])

   • Calculate ( s(1.01) ):
     • ( s(1.01) = -16(1.01)^2 + 111(1.01) = -16(1.0201) + 112.11 = -16.3216 + 112.11 = 95.7884 )
   • Use the average velocity formula: $$ V_{avg}[1, 1.01] = \frac{95.7884 - 95}{1.01 - 1} = \frac{0.7884}{0.01} = 78.84 $$

7. Find Average Velocity for Time Interval ([1, 1.001])

   • Calculate ( s(1.001) ):
     • ( s(1.001) = -16(1.001)^2 + 111(1.001) = -16(1.002001) + 111.111 = -16.032016 + 111.111 = 95.078984 )
   • Use the average velocity formula: $$ V_{avg}[1, 1.001] = \frac{95.078984 - 95}{1.001 - 1} = \frac{0.078984}{0.001} = 78.984 $$