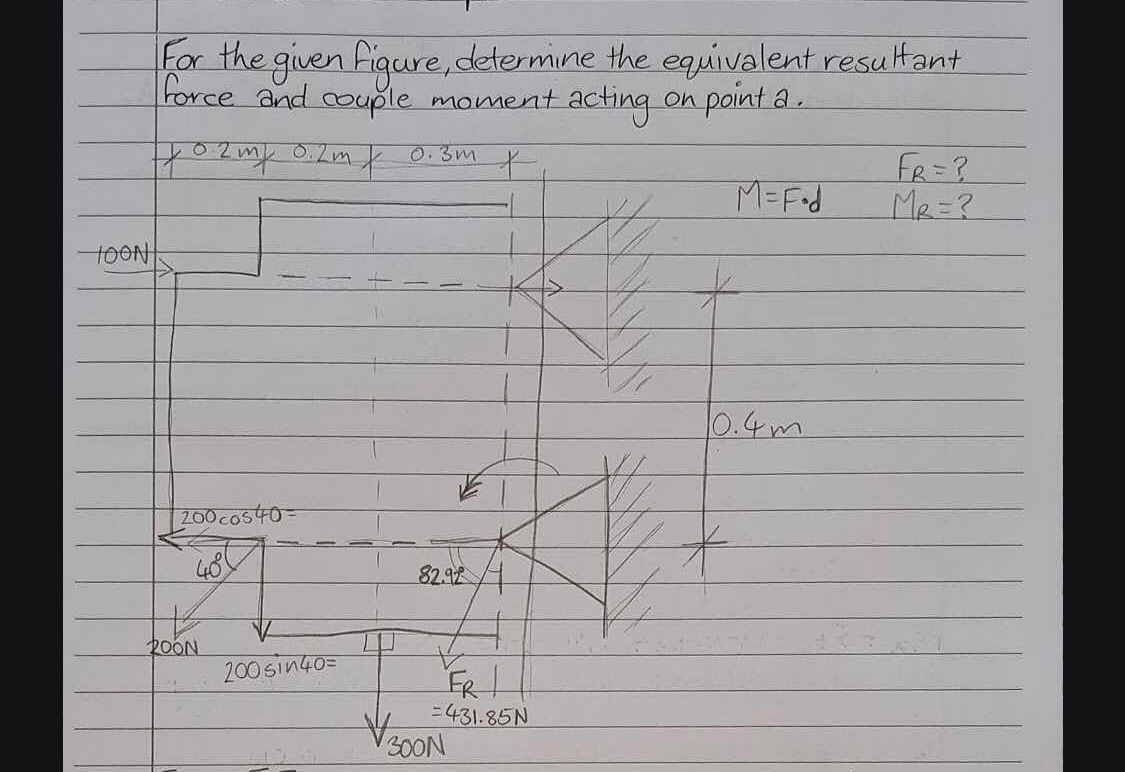
For the given figure, determine the equivalent resultant force and couple moment acting on point A.

Steps to Solve

1. Identify the Forces Acting on the Structure

The given forces acting on the structure are:

• A downward force of $100 , \text{N}$ at the left.
• A downward force of $200 , \text{N}$ at an angle of $40^\circ$.
• A downward force of $300 , \text{N}$ at the bottom.

2. Resolve the Forces into Components

For the $200 , \text{N}$ force:

• The horizontal component ($F_{200x}$) is calculated as: $$ F_{200x} = 200 \cos(40^\circ) $$
• The vertical component ($F_{200y}$) is calculated as: $$ F_{200y} = 200 \sin(40^\circ) $$

3. Calculate the Resultant Force

To find the equivalent resultant force ($F_R$), sum the vertical components from all forces:

• Total vertical force ($F_{total}$) is: $$ F_{total} = 100 + F_{200y} + 300 $$

4. Find the Magnitude of Resultant Force

Substituting in the values from the previous calculation: $$ F_R = \sqrt{F_{total}^2 + F_{200x}^2} $$

5. Calculate the Moments about Point A

The moment due to each force around point A can be calculated as:

• For the $100 , \text{N}$ force: $$ M_{100} = -100 \times 0.2 $$

• For the $200 , \text{N}$ force, consider the moment arm (vertical distance): $$ M_{200} = -200 \sin(40^\circ) \times (0.4) $$

• For the $300 , \text{N}$ force: $$ M_{300} = -300 \times (0.2 + 0.3) $$

6. Sum the Moments to Get Total Moment

The total moment around point A ($M_T$) is: $$ M_T = M_{100} + M_{200} + M_{300} $$