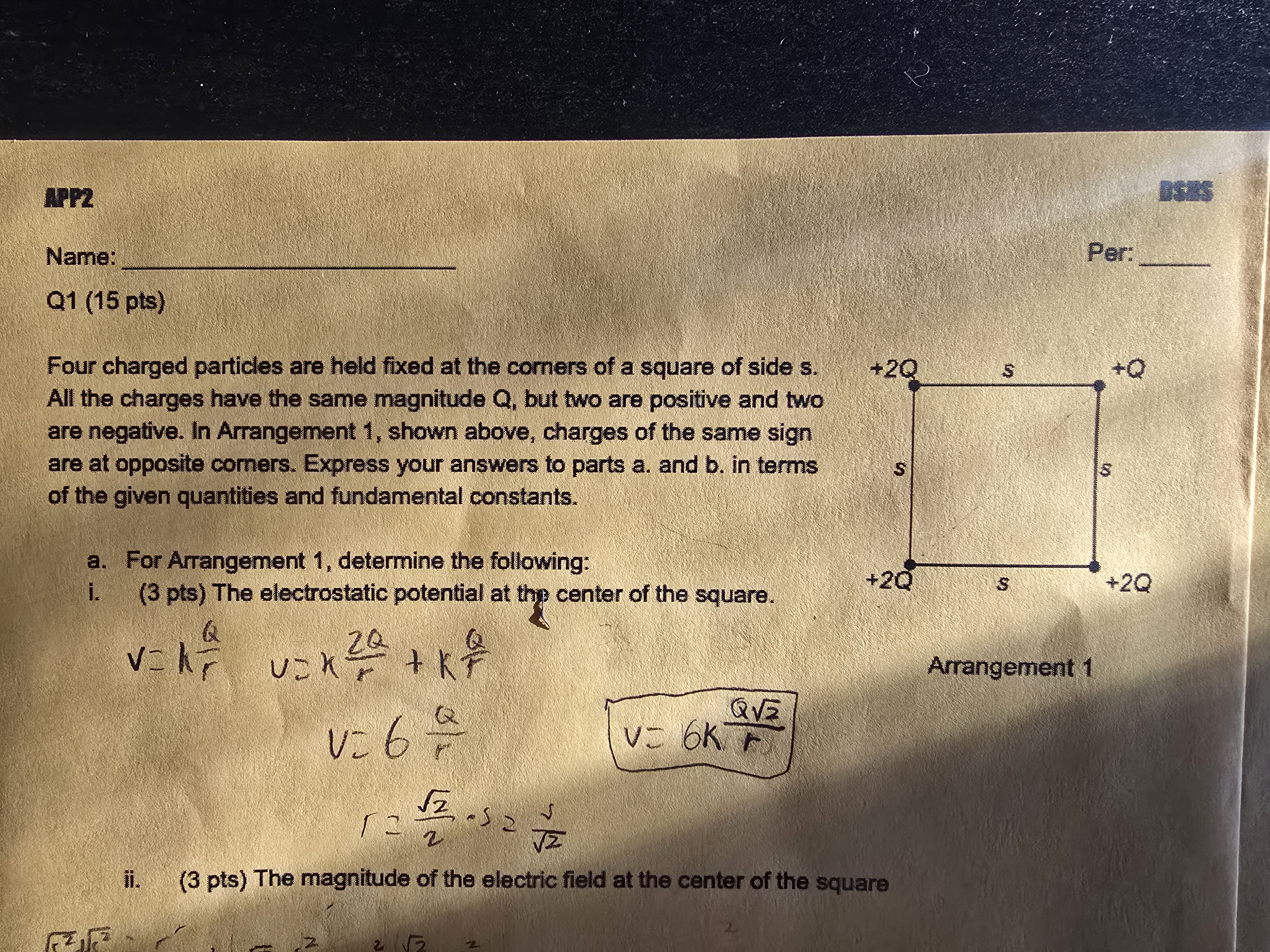
For Arrangement 1, determine the following: (3 pts) The electrostatic potential at the center of the square.
Understand the Problem
The question asks to determine the electrostatic potential at the center of a square formed by four charged particles located at the corners. The equation given needs to be simplified using the electrical potential produced by point charges.
Answer
$$ V = k \frac{2Q \sqrt{2}}{s} $$
Answer for screen readers
The electrostatic potential at the center of the square is: $$V = k \frac{2Q \sqrt{2}}{s}$$
Steps to Solve
-
Understand the configuration of the charges The charges are arranged as follows: at two opposite corners, there are charges of +2Q, and at the other two opposite corners, there are charges of -Q. The distance from each corner to the center of the square (where we calculate the potential) is given by the formula for the diagonal of the square: $$r = \frac{s}{\sqrt{2}}$$ where $s$ is the side length of the square.
-
Use the formula for electrostatic potential The electrostatic potential $V$ at a point due to a single point charge $Q$ is given by: $$V = k \frac{Q}{r}$$ where $k$ is Coulomb's constant.
-
Calculate the potential due to each charge at the center For each +2Q charge, the potential at the center is: $$V_{+2Q} = k \frac{2Q}{\frac{s}{\sqrt{2}}} = k \frac{2Q \sqrt{2}}{s}$$ Since there are two such charges: $$V_{total, +2Q} = 2 \left( k \frac{2Q \sqrt{2}}{s} \right) = k \frac{4Q \sqrt{2}}{s}$$
For each -Q charge, the potential at the center is: $$V_{-Q} = k \frac{-Q}{\frac{s}{\sqrt{2}}} = -k \frac{Q \sqrt{2}}{s}$$ Since there are two such charges: $$V_{total, -Q} = 2 \left( -k \frac{Q \sqrt{2}}{s} \right) = -k \frac{2Q \sqrt{2}}{s}$$
- Combine the potentials from all charges The total potential $V_{total}$ at the center is the sum of the potentials from all charges: $$V_{total} = V_{total, +2Q} + V_{total, -Q}$$ Substituting the expressions we derived: $$V_{total} = k \frac{4Q \sqrt{2}}{s} - k \frac{2Q \sqrt{2}}{s} = k \frac{(4Q - 2Q) \sqrt{2}}{s}$$ This simplifies to: $$V_{total} = k \frac{2Q \sqrt{2}}{s}$$
The electrostatic potential at the center of the square is: $$V = k \frac{2Q \sqrt{2}}{s}$$
More Information
This result represents the total electrostatic potential resulting from the arrangement of the four charges located at the corners of the square. The use of Coulomb's law for potential calculations is fundamental in electrostatics, and this particular arrangement demonstrates the principle of superposition, where the total potential is the sum of the potentials from individual charges.
Tips
- Forgetting to account for direction: Some may forget that potentials due to positive and negative charges contribute differently, but potential is scalar, so we only sum the magnitudes.
- Using incorrect distances: Confusing the distance to the center with the length of the square edges can lead to erroneous calculations. Always verify the diagonal distance.
- Neglecting the number of charges: It's important to remember how many of each type of charge are contributing to the total potential.
