Factorise x² + 2x - 8
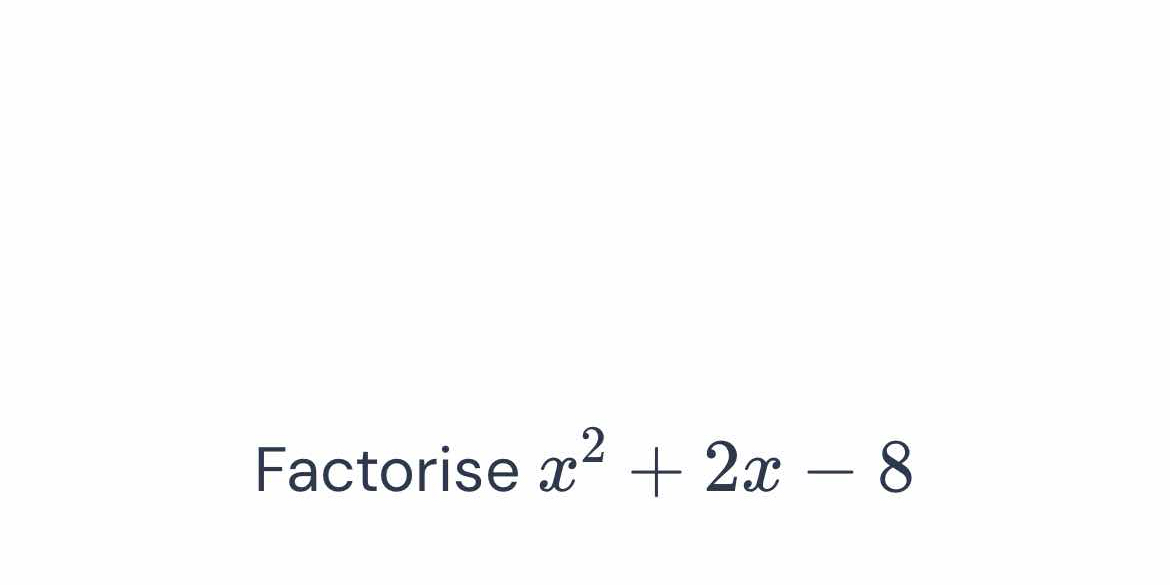
Understand the Problem
The question is asking us to factor the quadratic expression x² + 2x - 8, which involves finding two binomials that multiply to give this expression.
Answer
The factored form is \( (x + 4)(x - 2) \).
Answer for screen readers
The factored form of ( x^2 + 2x - 8 ) is ( (x + 4)(x - 2) ).
Steps to Solve
-
Identify the quadratic expression We have the quadratic expression ( x^2 + 2x - 8 ).
-
Find two numbers that multiply and add We need to find two numbers that multiply to give the product of the constant term (-8) and the leading coefficient (1), which is ( -8 ), and add up to the coefficient of the linear term (2).
-
Determine the factors The two numbers that satisfy these conditions are ( 4 ) and ( -2 ):
- ( 4 \times -2 = -8 )
- ( 4 + (-2) = 2 )
- Write the factors as binomials We can now express the quadratic as a product of two binomials: $$ (x + 4)(x - 2) $$
The factored form of ( x^2 + 2x - 8 ) is ( (x + 4)(x - 2) ).
More Information
Factoring is a useful algebraic technique to simplify expressions and solve equations. Knowing how to factor quadratics can greatly aid in solving quadratic equations and understanding functions.
Tips
One common mistake when factoring quadratics is overlooking the signs of the factors. Always double-check the multiplication and addition conditions of the factors.
AI-generated content may contain errors. Please verify critical information