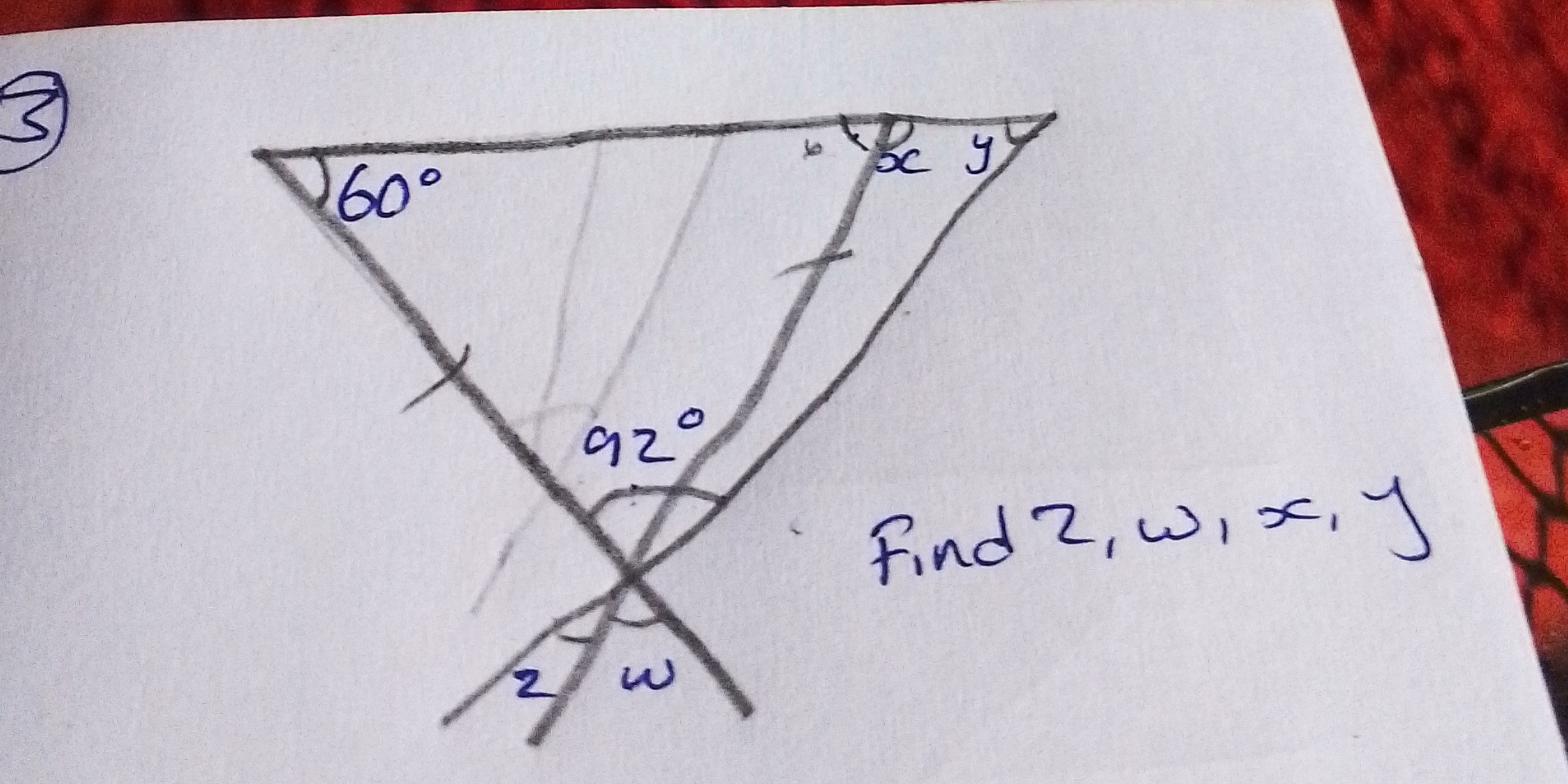
Find z, w, x, y.
Understand the Problem
The question involves finding the values of z, w, x, and y based on the angles given in a geometric configuration. The angles 60° and 92° suggest relationships between the angles that need to be applied to find the unknowns.
Answer
The values are: $z = 120°$, $w = 92°$, $x = 60°$, $y = 88°$.
Answer for screen readers
The values are:
- $z = 120°$
- $w = 92°$
- $x = 60°$
- $y = 88°$
Steps to Solve
-
Identify Relationships Between Angles In the diagram, the angles are formed by intersecting lines. Recognize that the angles formed opposite to each other at the intersection are equal.
-
Determine Angle Relationships We know that:
- The angle opposite to the 60° angle is also 60°.
- Since the angles on a straight line sum up to 180°, we can find the value of angle $z$:
$$ z + 60° = 180° $$
-
Solve for z Rearranging the equation from the previous step gives:
$$ z = 180° - 60° = 120° $$
-
Calculate angle w The angle w, opposite to 92°, will also be 92° due to the property of vertically opposite angles.
-
Determine angles x and y Both angles $x$ and $y$ are supplementary to angles $z$ and $w$ respectively:
For angle x:
$$ x + z = 180° $$
Hence,
$$ x = 180° - z = 180° - 120° = 60° $$
For angle y:
$$ y + w = 180° $$
Hence,
$$ y = 180° - w = 180° - 92° = 88° $$
The values are:
- $z = 120°$
- $w = 92°$
- $x = 60°$
- $y = 88°$
More Information
The angles in the configuration relate to one another through properties of vertical and supplementary angles. Understanding these relationships helps in solving geometric problems effectively.
Tips
- Ignoring angle relationships: Some might overlook the equality of vertically opposite angles. Ensure you recognize this property.
- Miscalculating supplementary angles: Always remember that supplementary angles sum to 180°, so double-check subtraction when solving for angles.
AI-generated content may contain errors. Please verify critical information